Editorial for An Animal Contest 7 P5 - Squirrel Scheming

Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.

Author: dxke02

Hint 1

Consider the following problem: Given an arbitrarily rooted tree, what is the minimum distance of a path that starts from the root, visits every single node once then returns to the root?

Answer

The answer is $2 \times E$ ~2 \times E~ where $E$ ~E~ is the number of edges in the tree. We traverse each edge once when entering a subtree, and another time when leaving the subtree to return to the root. Overall, we traverse each edge twice so the answer is $2 \times E$ ~2 \times E~.

Hint 2

If we don't consider the lexicographic part of the problem, this problem is the exact same as the above except we don't need to return to the root. Think about the maximum distance we can "save" from not returning to the root.

Answer

The maximum distance we can "save" is equal to the diameter of the tree. Which means the minimum cost path is equal to $2 \times E - D$ ~2 \times E - D~ where $E$ ~E~ is the number of edges, and $D$ ~D~ is the diameter of the tree.

Hint 3

Find the optimal starting node for a permutation, then build the rest of the permutation.

Subtask 1

Let's first find the optimal starting node in the permutation. This node is simply the minimum node that is an endpoint of any diameter in the tree. To find this node, one can simply run a DP on the tree. Let's call this node $F$ ~F~.

Next, observe that for any diameter $(F, v)$ ~(F, v)~, there is a permutation where $v$ ~v~ is the last node and achieves the minimum cost. This is because after we visit $v$ ~v~ we do not need to return to $F$ ~F~ thus saving a cost equal to the length of the diameter of the tree, which is the maximum amount you can save.

This encourages a solution that first fixes the start node and the end node, then constructs the rest of the permutation. As it turns out, knowing the first and last node of the permutation makes the problem a lot simpler.

To get an idea of what the algorithm looks like, consider the following tree:

Diagram

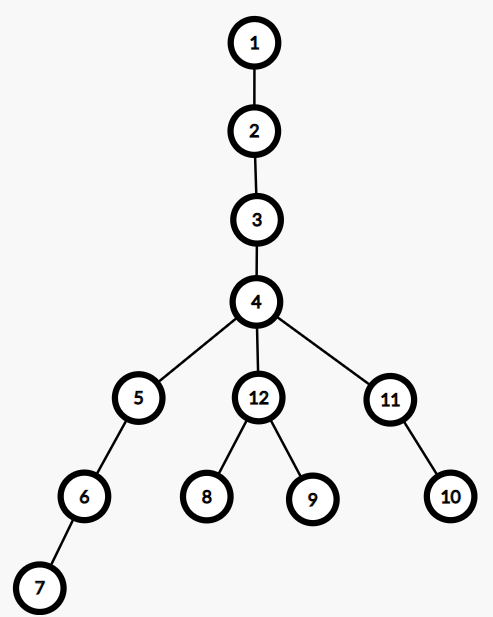
Clearly, the optimal starting node is $1$ and the only diameter we need to consider is $(1, 7)$ . Now, let's recursively build the permutation starting from $1$ . For each recursive call to a node $v$ , let's sort all of $v$ 's children by the minimum value in each child's subtree. After sorting the children, go through the children in increasing order of value. At each child, recursively call the function to the node with the minimum value in that child's subtree. However, we must still consider one final detail: we must end the permutation on the diameter that was fixed. So, when sorting we must also check if any of the subtrees contain the ending node of the permutation. If it exists in a subtree, we must process that subtree last no matter what the minimum value present in the subtree is. After processing all the children, we must return to the original node that the function was called from. For example, in the diagram above, when processing node $4$ , we can see that the ordering of the subtrees will be $[12, 11, 5]$ (diameter $(1, 7)$ is present in $5$ 's subtree so we automatically process it last). So, we will call the function at node $8$ because it is the minimum value in $12$ 's subtree. After processing $8$ , we must return back to node $4$ . However, if we return directly, then we cannot process any other nodes in $4$ 's subtree because of the property that every subtree will be entered and exited at most once. Therefore, we must call the function at $8$ 's parent. After we call $12$ , we can again sort all the nodes in its subtree, ignoring $8$ because we already processed $8$ , and then recursively call the function on all of the sorted nodes. To keep track of which subtrees to ignore and where to stop calling the function to the parent, pass parameters that keep track of which children have been visited already as well as which node initially called the search into the subtree. Finally, we can run this function for each possible diameter that stems from the optimal starting node and compare their outputs.

Time Complexity: $\mathcal O(N^2 \log N)$ ~\mathcal O(N^2 \log N)~

Subtask 2

Since there are $\mathcal O(N)$ ~\mathcal O(N)~ diameters in the worst case, we can no longer afford to run the algorithm directly for each diameter. To optimize, instead of fixing the diameter, we can actually make our sorting slightly more sophisticated to find an optimal diameter. As with the previous algorithm, sort the nodes by the minimum node present in each subtree. However, this time also keep track of which subtrees contain at least one ending of a diameter. Now, instead of fixing the diameter, we can simply process the maximum value subtree that contains at least $1$ ~1~ diameter last.

Time Complexity: $\mathcal O(N \log N)$ ~\mathcal O(N \log N)~

Comments

There are no comments at the moment.