ACSL '09 Practice P7 - Cube
View as PDFACSL Practice 2009
Folding six squares connected in some special ways can form a cube. For
example, in the diagram below, the six squares on the left can be folded
into a cube (with face
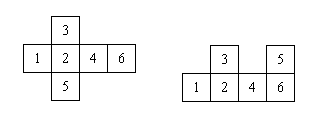
A
0 0 0 0 0 0 0 0 0 0 0 0
0 3 0 5 0 0 0 0 0 0 0 0
1 2 4 6 0 0 0 0 0 0 5 6
0 0 0 0 0 0 0 0 0 0 0 4
0 0 0 0 0 0 0 0 0 0 3 2
0 0 0 0 0 0 0 0 0 0 0 1Given a square representation, determine if the squares can be folded
into a cube; if so, find the face opposite face
Input Specification
The input consists of six lines with each line containing six integers.
All but six of the input integers are zeros. The non-zero integers are
Output Specification
The output file consists of a single integer. The integer is 0 if the
squares cannot be folded into a cube; otherwise, the integer is the
number of the face opposite face
Sample Input
0 0 0 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0
0 5 2 3 0 0
0 0 4 0 0 0
0 0 6 0 0 0Sample Output
4Diagram
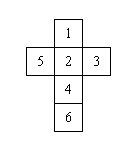
Comments