Editorial for APIO '10 P3 - Signaling
Submitting an official solution before solving the problem yourself is a bannable offence.
The problem description is: Given points on a 2D plane, we guarantee that any three points are not in a line and any four points are not on a circle. Randomly pick
different points to make a circle, and compute the average number of points that are inside or on the circle. We assume that each point has the same probability to be chosen.
Our goal is to compute the average number of points that are covered by the circle. In fact, we only need to compute the sum of points that are covered by any circle and divide the result by to get the exact answer for our problem.
Algorithm 1: A brute force solution for this problem is to enumerate any three different points and calculate their corresponding circumcircle. Then we can count how many points are inside or on the circle in time. Clearly, this solution works in time
.
Now our task is to count the number of quadruplets such that point
is inside the circumcircle of
. Let's consider the position relation between
and
:
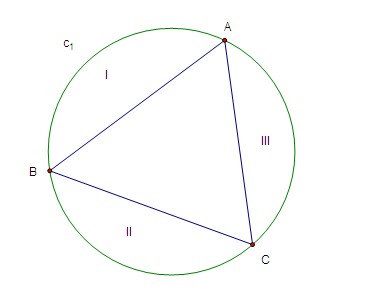
Seeing the above figure, we can deduce that if point is in area I, II, or III, then the sum of the angle
and the angle of the opposite point must be
since the interior angle is always larger than the corresponding circumferential angle. For example, if
is in area I, then
and the four points must form a convex quadrangle. Similarly, if
is outside the circle, the sum of the angle
and the corresponding opposite angle must be
. And another case is
is inside the triangle
, then the four points must form a concave quadrangle.
Hence let's consider every quadrangle we get from the set of points, note that two quadrangles are distinct if and only if the set of the points are different (
points can construct different quadrangles if one point is inside the triangle of another
points). We can see that
- if it's convex, then there are
ways to pick
points to make a circle so that the circle contains the remaining point. This is because the sum of the
angles is equal to
and no
points are on a circle, there must be exactly a pair of opposite angles such that their sum is greater than
. For example, if
in a quadrangle
, then point
must be in the circle of
while
must be in the circle of
.
- if it's concave, then there is exactly
way to pick
points to make a circle such that the circle contains the remaining point. In this case, the
point must be in the triangle of the other
points.
Let the number of convex quadrangles and
the number of concave quadrangles. Our new goal is to compute the value of
and it is straightforward that
. There are many ways to compute
or
or any linear combinations of
and
in
or
time, then we can get
. Next, we will give a very simple method to compute
.
For any quadrangle and a vertex
of
, if we can draw a line through
such that all other
points lie in one side of this line, then we say that the vertex
is "good".
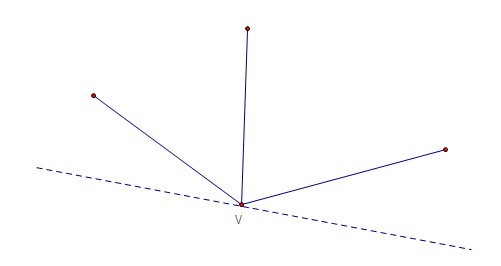
We can see that for any convex quadrangle, all vertices are "good" while there are only "good" vertices in a concave quadrangle except the innermost point. If we can count the number of "good" points for any
points, then we have got the value of
.
Algorithm 2: enumerate a point as , and sort all other points by their polar angles with respect to
. Then we can scan all other points in the order and maintain the number of points such that the angle between it and the current point is
. Then we can count the number of quadrangles in which
is a "good" vertex in
time. For each point
, it takes
time to sort all other points by polar angles and
time to scan all points to get the answer. So the total running time is
.
Till now, we have got a complete algorithm in time. In fact, there are many similar methods to compute a linear combination of
and
and after we sort all other
points, we can enumerate two points to calculate the result to get an
algorithm which can pass
of the test cases.
Comments