First, let's consider a solution with ~\mathcal O(n \times maxX)~ complexity. It's a simple dynamic programming approach.

We have an array ~dyn~ (size ~maxX~), which should say how costly would it be to be in this position at the end of the turn. At initialization, each position is set to ~maxValue~ (some big number), except the initial position which is set to be ~0~. This should represent that in the initial moment it's impossible to be anywhere except in the initial position.

Before each turn we can change position, so before each turn we could calculate the best cost of being in that position when the bulbs light up. We can do this by passing this array twice – once from the left and once from the right. Consider the case we're passing from left to right (smaller index ~i~ to larger index ~i~, the other case could be explained in a similar fashion). While passing, we can keep the ~bestVal~, which would be initiated to ~dyn[0]~, and updated as ~bestVal = \min(bestVal+1, dyn[i])~, ~dyn[i] = bestVal~ for each ~i > 0~. Rationale: if we came from the ~i-1~ position, we have the same cost of that position ~+1~. If we didn't, we have the same cost we had before this. Now we only need to add distance to the closest bulb for each position and we finished this turn. When we finish each turn we pick the lowest value in the array, and that's our solution. Simple enough.

But this solution is too slow for us. We want more.

Statement: We never have to move to the position which is not the beginning or end position of one of the light-ups.

Let's consider the following situation: We're at the position ~x~. If ~x~ is going to be inside of the next turn shining bulbs, there's no point in moving at all (it would be the same as moving after the turn). So, consider ~x~ is outside those bulbs, and ~x_{closest}~ is the closest bulb to ~x~ that will be lighten-up. Also, consider ~x < x_{closest}~ (the other case could be explained in a similar fashion). Consider all the remaining light-up points (light-up beginning and end positions) are in the array ~pos~, which is sorted. Take a look at the following picture:

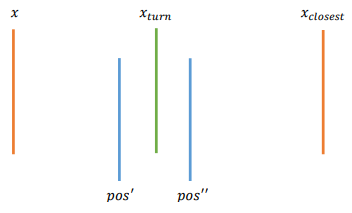
First thing we could notice is the fact that our cost for this turn is going to be ~x_{closest}-x~, if we finish the turn anywhere between ~x~ and ~x_{closest}~ inclusive. Going left from ~x~ or right from ~x_{closest}~ doesn't make any sense, because we would have the same or bigger cost than staying in ~x~ or ~x_{closest}~ and moving from it in the next turn.

Next, let's consider we haven't ended our turn on some light-up endpoint, but between two neighboring endpoints, ~pos'~ and ~pos''~. Let's call that position ~x_{turn}~. Let's also introduce ~x_{closest2}~, which is the closest bulb from the ~x_{turn}~ in the next turn light-up.

If ~x_{turn}~ is shining, then ~pos'~ is shining as well, so we could have finished our turn there. If ~x_{closer2} \le pos'~ we would be better off or equally well if we finished our turn in ~pos'~. In that case, we would have ~x_{turn}-pos'~ smaller cost for the next turn. If afterwards we need to go to ~x_{turn}~, total cost would not exceed the cost of going straight to ~x_{turn}~ in the initial turn. If ~x_{closer2} \ge pos''~ we would be better off or equally well if we finished our turn in ~pos''~, similar to the explanation for ~pos'~. So, in each turn we could stay in the place or go to the closest light-up endpoint and we could still get the optimal solution.

We can use this fact to make an ~\mathcal O(n^2)~ solution – instead of each position we should take consider only light-up endpoints and initial position. Everything else is the same as in the original solution.

Dynamic programming solution is enough to pass within the constraints for the program, but this problem can be solved in linear time as well.

Let's look at the values of array ~dyn~. We can notice that this array actually has only one "local minimum" at each turn. What this means is that we have a range ~[l, r]~ and that all of the values from ~dyn[0]~ to ~dyn[l]~ are monotonically decreasing, all values from ~dyn[r]~ to ~dyn[10^9]~ are monotonically increasing, while all of the values ~dyn[l], dyn[l+1], \dots, dyn[r]~ have the same value and represent the minimum summed cost until this turn. We can use this property to create a linear time algorithm.

Our linear algorithm will be as follows:

At the beginning, our optimal range will be ~[x_{start}, x_{start}]~ and minimum cost will be ~0~. At each turn, we will update this optimal range and minimum cost.

If the range of shining bulbs in the next turn intersects with our optimal range, we can easily see that our new optimal range will be this intersection. The minimum cost will stay the same as the cost for previous turn, since we don't need to move if we are located somewhere in this intersection, as we will already be located at a bulb that is shining. Anywhere outside of this intersection, the cost would increase since either the distance to the closest shining bulb would be larger than ~0~, or because of moving from our optimal range to somewhere outside of it, or both.

If the range of shining bulbs in the next turn does not intersect our optimal range and is left from it, we will set that our optimal range starts from the rightmost shining bulb and ends at the left end of our previously optimal range. Our minimum cost will increase for exactly the distance between these positions – if we don't move from the left end of our previously optimal range, our cost increases for this distance. If we move from the left end of our previously optimal range by one position to the left, we decrease our distance in the next turn by ~1~, but increase the cost by ~1~ because of the move. Same goes for moving two positions to left, and so on until the movement to the rightmost shining bulb in the next turn (at which point our distance to a shining bulb will be ~0~, but our cost for moving will be the same as distance when we didn't move at all). It is easily seen that the minimum cost for a position that is left from this new optimal range is larger by ~1~, and the minimum cost for a position that is right from this new optimal range is also larger by ~1~. Moving further to the left or right, this cost increases more and more, resulting in only one "local minimum" as we described before.

If the range of shining bulbs does not intersect our optimal range and is right from it, we can do a similar thing as we do when the range is left from our optimal range.

After all the turns, we have our optimal range and the minimum cost possible. The total complexity is ~\mathcal O(n)~, since in each turn we update the range in ~\mathcal O(1)~.