The solution to this task effectively consists of two parts: analyzing the geometry and the relations between the two polygons, and deriving whether they intersect or not.

For the second part, we need to find all intersections between each of the polygons and the common line of their two planes. Once that is done, and the intersection points along the line are sorted, we can simply go through them and count the number of intersections of, say, polygon ~P_1~ with the inside of polygon ~P_2~, as well as keep track of the directions in which it passes through ~P_2~. Whenever we reach a point belonging to polygon ~P_2~, our position (inside or outside of polygon ~P_2~) changes. Now we simply count points belonging to polygon ~P_1~, which we reach while being inside of the polygon ~P_2~. This solution has the complexity of ~\mathcal O(N \log N)~, where ~N~ is the sum of the edges of the two polygons.

As for the geometry – it seems that an approach using vectors (the mathematical ones, not arrays with variable length) is much easier than the others. It relieves the coder from having to solve complicated equations, but instead uses relatively simple calculus, once all the vector operations have been defined. Thus, we first define the vectors of the two polygons' planes as the vector product of two consecutive edges' vectors. The two consecutive vectors will be used as the base of the 2D vector space defined by the plane. Then, for each edge of both polygons, we need to see whether it has intersections with the other polygon's plane or not. Let's observe the case when the edge's end points (let's label them ~A~ and ~B~) are on the opposite sides of the plane (~\alpha~). If the angle between ~\alpha~'s direction vector and the vector from ~A~ to a random point in ~\alpha~ is acute, then the angle between ~\alpha~'s direction vector and the vector from ~B~ to the same point will be obtuse, and vice-versa. Thus, if the dot products of the two vectors for both ~A~ and ~B~ are of different sign, they are on the opposite side of ~\alpha~ and there is an intersection. If either of the products is zero, then the corresponding point is inside ~\alpha~ (this case will be discussed later on).

Finding the point of intersection (point ~X~) between line ~AB~ and ~\alpha~ can be done in several ways. One solution is to pick a random point in ~\alpha~ (point ~C~) and observe the vector ~CA~. It is easy to see that one can represent it as a linear combination of ~\alpha~'s base vectors and the vector ~AB~. Once the parameters of the linear combination have been found by solving the system of equations (determinants seem easiest), one can simply ignore the component associated with the vector ~AB~. The rest will sum up to the vector ~CX~, and thus ~X~ is found. It can also be done with even simpler expressions using vectors (left to the reader to find out), but this solution seemed very intuitive and easy to code, so I stuck with it.

The only special case happens when a polygon's vertex lies exactly on the other polygon's plane. In that case, one simply observes the previous and the next vertex and whether they are on the opposite sides of the plane or not. If they are – the intersection is taken as the "problematic" point and if they are not, we assume there is no intersection. See Picture 1 and Picture 2. Similar applies when two consecutive points are lying on the plane. Please note that simply ignoring the point lying on the other polygon's plane is wrong.

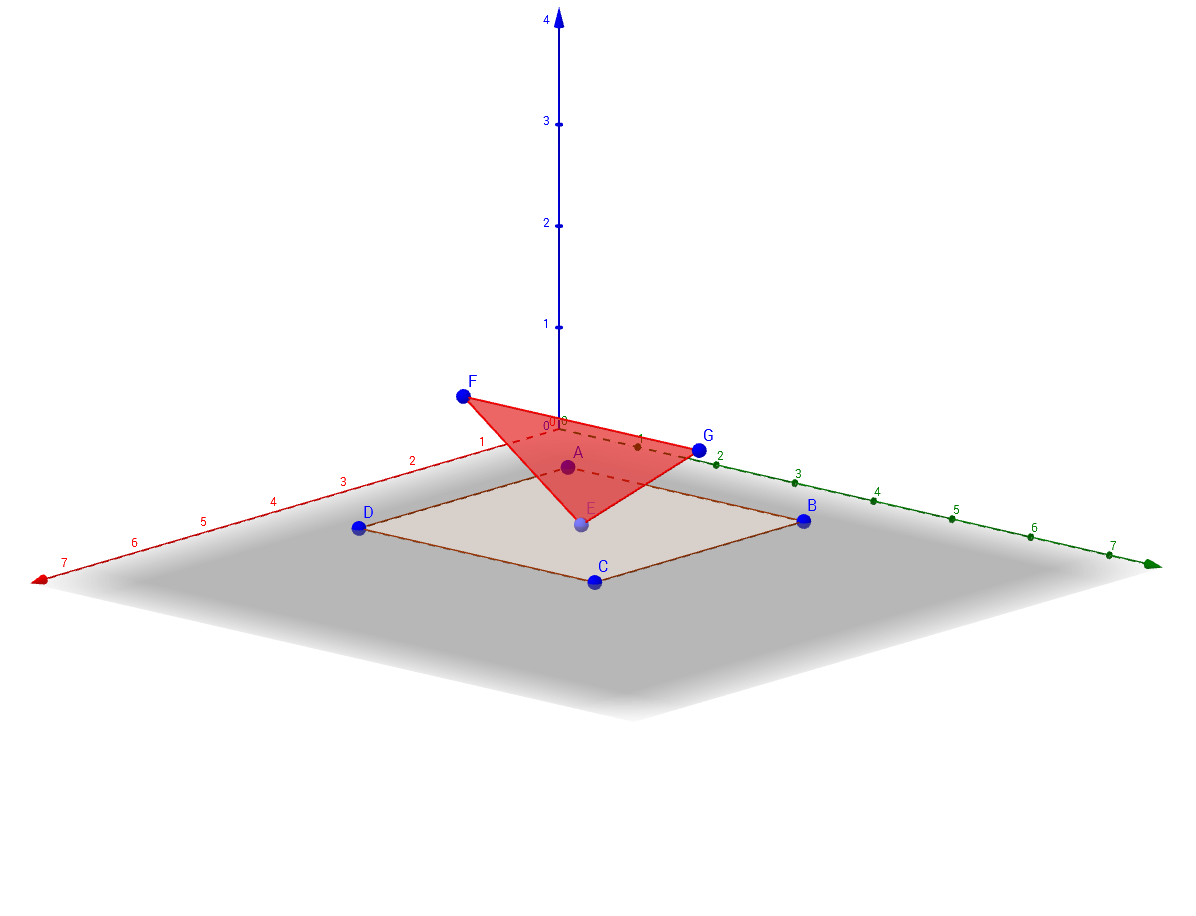
Picture 1: Point ~E~ is on the plane of ~ABCD~ polygon. ~FG~ segment doesn't intersect ~ABCD~ polygon, so ~E~ is not a point of intersection.

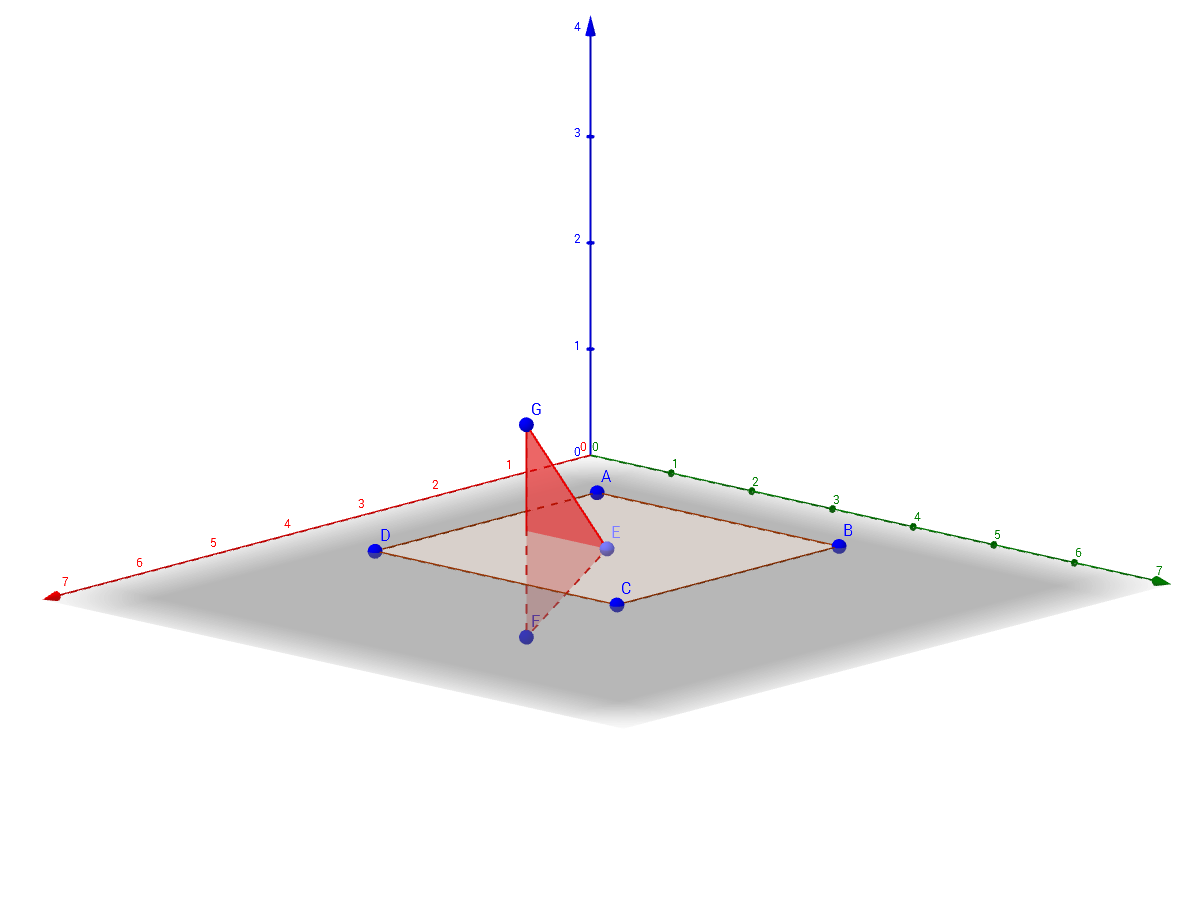
Picture 2: Point ~E~ is on the plane of ~ABCD~ polygon. In this case, ~FG~ segment intersects ~ABCD~ polygon, so ~E~ is a point of intersection.