In the basic case (when ~X = 1~) we have a common DP problem. Unfortunately, for larger ~X~ it is much more complicated, so the basic case cannot be generalized.

Instead, we can look at this problem as a graph problem. We represent the crossword as a directed weighted graph, where edges have both a cost and a capacity. First, we represent every letter from the crossword as a vertex, and add an extra source and sink node. Then, we connect each letter's vertex with the next one with an edge of capacity ~\infty~ and cost ~0~. Also, we connect the source node with the first letter and we connect the last letter with the sink node using the same kind of edge. Finally, for every position where one of the given words matches a substring, we connect the first letter of the match with a letter just after the end of the match with an edge of capacity ~1~ and a cost equal to the score we get for the word. By doing it for an example input we get this graph:

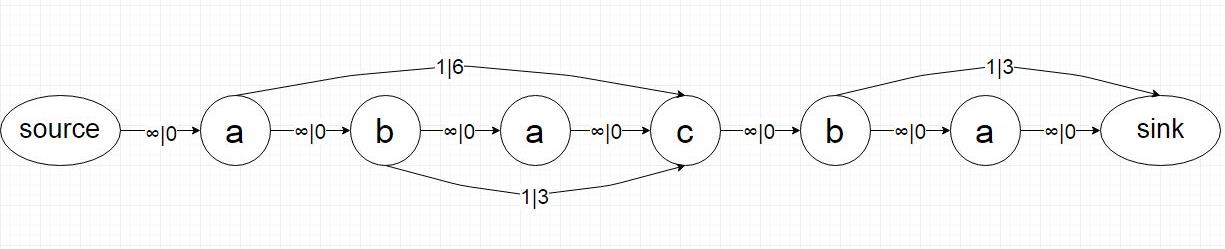
Any flow with total capacity ~X~ is equivalent to a set of selected words that satisfies the given constraint, since we can have at most ~X~ "overlapping" ~1~-capacity edges. The problem now reduces to maximizing the cost of that flow, which can be done by adapting an algorithm that solves the min-cost flow problem (by using negative values). Using an adaptation of the Bellman-Ford algorithm we can get a complexity of ~\mathcal O(E^2 V \log V)~.