Editorial for Balkan OI '11 P5 - Time Is Money
Submitting an official solution before solving the problem yourself is a bannable offence.
When , the problem is a simple minimum spanning tree, because minimizing
is the same as minimizing
.
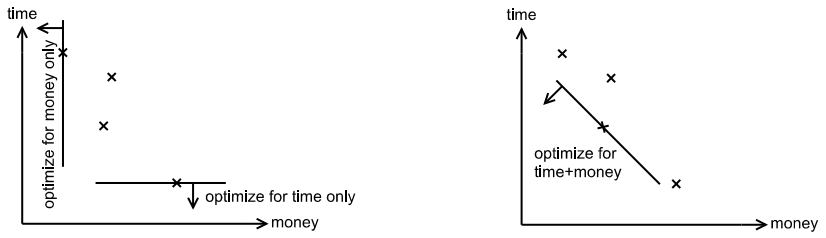
When and
are different, different solutions can generate different trade-offs between
and
. It is straightforward to optimize for
only or
only, and it is also straightforward to optimize for
, because the sum in the total cost can be distributed to sums over individual links:
.
The next step is to optimize for a weighted sum of and
,
. This corresponds in the solution space to point left-most of a line with the slope
. By varying the
ratio the lower convex hull of points in the solution space can be determined.
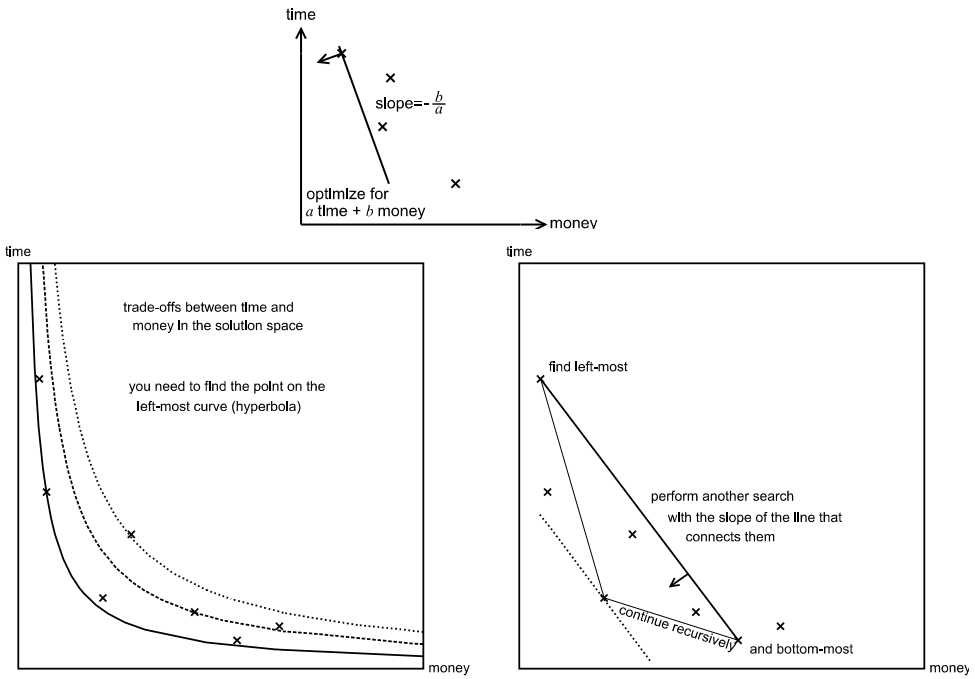
This already leads to a simple solution which consists of sweeping the range of values for but we do not know yet when the sweep is fine-grained enough to determine all points. A more precise approach consists of finding a solution which optimizes time, a solution optimizing money and then using the slope of the line connecting them. You then continue recursively for the two pairs formed by the new solution with the previous solution. You stop when you don't find a new solution which is not already colinear to the two points.
Finding the points on the lower convex hull is sufficient because the curve defining solutions of equal cost is convex (a hyperbola, ). The number of points on the lower convex hull is limited by the fact that coordinates are integer (maximum
) and the slope between consecutive points on the hull has to vary.
Comments