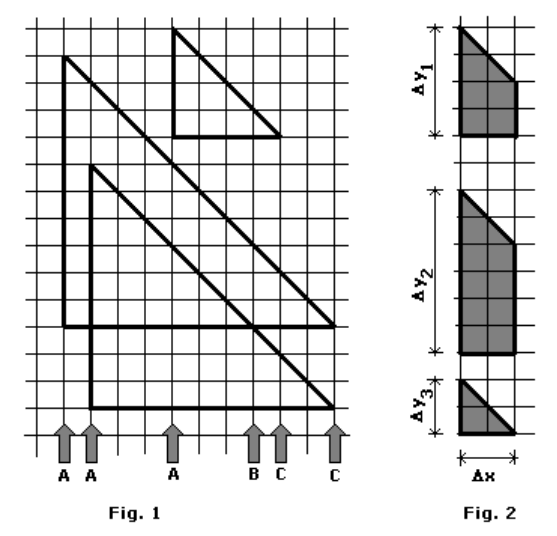
We can use a plane sweep method sweeping from left to right. There are three kinds of event points for the algorithm (denoted in Figure 1 by gray arrows):

• beginning of new triangle (value $x_i$ from description);
• crossing point of one triangle horizontal edge with others hypotenuse;
• rightmost vertex of some triangle (value $x_i+m_i$ from task description).

If we look at these event points consecutively, we can calculate common area increasing, if we at each event point $x_k$ know number $n_k$ of actual line segments and sum of their lengths $s_k=\sum \mathrm{\Delta }{y}_i$, where $\mathrm{\Delta }{y}_i$ is the length of one segment. Example with three segments are shown in Figure 2.

Then increment for each gap between two neighbour event points $(\mathrm{\Delta }x=x_{k+1}-x_k)$ can be calculated as $s_k\mathrm{\Delta }x-n_k\frac{(\mathrm{\Delta }x{)}^2}{2}$. Performing sweeping from left to right and summing up these increments we finally obtain total common area of all triangles.