Baltic Olympiad in Informatics: 2004 Day 2, Problem 2

Example with ~8~ rectangles. The segment ~AB~ crosses ~5~ of them.

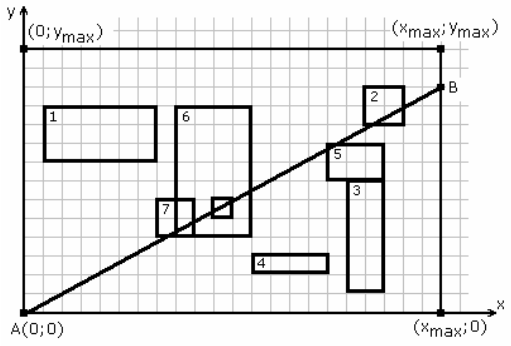
There are given ~N~ rectangles on the plane. Rectangle sides are parallel to coordinate axis. These rectangles may overlap, coincide or be drawn inside one another. Their vertices have non-negative integer coordinates and ~x~ coordinates do not exceed ~x_\text{max}~ and ~y~ coordinates do not exceed ~y_\text{max}~.

A segment is started in the point ~A(0, 0)~ and ended in point ~B~. The coordinates of the point ~B~ (the other end of the segment) satisfy the following conditions:

• The coordinates of ~B~ are integer numbers;
• The point ~B~ belongs either to the segment ~[(0, y_\text{max}), (x_\text{max}, y_\text{max})]~ or to the segment ~[(x_\text{max}, 0), (x_\text{max}, y_\text{max})]~.

The segment ~AB~ might cross rectangles (we assume that crossing takes place even if only one rectangle vertex is crossed).

Write a program to find a point ~B~ for which the segment ~AB~ crosses as many rectangles as possible.

Constraints

~1 \le N \le 10^4~

~0 \le x_{bl} < x_{tr} \le x_\text{max} \le 10^9~

~0 \le y_{bl} < y_{tr} \le y_\text{max} \le 10^9~

Input Specification

The first line of the input contains three space-separated integers: ~x_\text{max}, y_\text{max}~ and ~N~.

Each of the following ~N~ lines contains four space-separated integers: the coordinates of the bottom left corner ~x_{bl}~ and ~y_{bl}~, and coordinates of the top right corner ~x_{tr}~ and ~y_{tr}~.

Output Specification

Output three space-separated integers on the first and only line of output.

First output the maximum number of crossed rectangles, followed by the ~x~ and ~y~ coordinates of point ~B~.

If there are several solutions, output any one of them.

Sample Input

22 14 8
1 8 7 11
18 10 20 12
17 1 19 7
12 2 16 3
16 7 19 9
8 4 12 11
7 4 9 6
10 5 11 6

Sample Output

5 22 12

Sample Explanation

The sample corresponds to the diagram in the problem statement. Another possible solution is 5 22 11.