Baltic OI '07 P4 - Building a Fence
View as PDFBaltic Olympiad in Informatics: 2007 Day 2, Problem 1
Leopold is indeed a lucky fellow. He just won a huge estate in the lottery. The estate contains several grand buildings in addition to the main mansion, in which he intends to live from now on. However, the estate lacks a fence protecting the premises from trespassers, which concerns Leopold to a great extent. He wants to build a fence and, in order to save money, he decides it is sufficient to have a fence that encloses the main mansion, except for one important restriction: the fence must not lie too close to any of the buildings. To be precise, seen from above, each building is enclosed in a surrounding forbidden rectangle within which no part of the fence may lie. The rectangles' sides are parallel to the x and y-axis. Each part of the fence must also be parallel either to the x-axis or the y-axis.
Help Leopold to compute the minimum length of any allowed fence enclosing the main mansion.
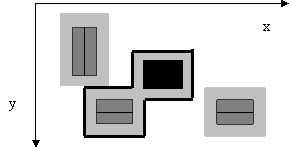
Figure 1: The main mansion (black) and three other buildings with surrounding forbidden rectangles. The thick black line shows a shortest allowed fence enclosing the main mansion.
Constraints
Subtask 1 [35%]
Subtask 2 [65%]
No additional constraints.
Input Specification
The first line contains a positive integer
Output Specification
Output the minimum length of any allowed fence enclosing the main mansion.
Sample Input
4
8 4 13 8
2 1 6 7
4 7 9 11
14 7 19 11Sample Output
32
Comments