Editorial for Baltic OI '10 P6 - Mines - DMOJ: Modern Online Judge

Editorial for Baltic OI '10 P6 - Mines

Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.

Consider the grid with $N$ ~N~ rows and $M$ ~M~ columns. Since we don't know how to solve cases when $N \equiv M \equiv 2 \pmod 3$ ~N \equiv M \equiv 2 \pmod 3~ efficiently, there were no such test cases given. Let's look at the solution for other cases. We may assume that $N \not\equiv 2 \pmod 3$ ~N \not\equiv 2 \pmod 3~. If $N \equiv 2 \pmod 3$ ~N \equiv 2 \pmod 3~ then $M \not\equiv 2 \pmod 3$ ~M \not\equiv 2 \pmod 3~ and we rotate the grid by $90^\circ$ ~90^\circ~.

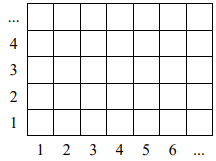
Let's number the rows from bottom to top and the columns from left to right. The cell with row number $x$ ~x~ and column number $y$ ~y~ is denoted by $(x, y)$ ~(x, y)~. By $A$ ~A~ we denote the table given in input and by $X$ ~X~ – the mine field we are looking for. We say $X(x, y) = 1$ ~X(x, y) = 1~ if there is a mine in cell $(x, y)$ ~(x, y)~ and $X(x, y) = 0$ ~X(x, y) = 0~ otherwise. We denote by $A(x, y)$ ~A(x, y)~ the total number of mines in cell $(x, y)$ ~(x, y)~ and its adjacent cells. Then, for instance, $A(1, 1) = X(1, 1)+X(1, 2)+X(2, 1)+X(2, 2)$ , $A(1, 2) = X(1, 1)+X(1, 2)+X(1, 3)+X(2, 1)+X(2, 2)+X(2, 3)$ and so on.

Let's first solve two subtasks:

Find the third row of the grid;
Solve the task for the grid of size $1 \times M$ ~1 \times M~.

Finding the third row of the grid

Note that:

$X(3, 3) = A(1, 1)+A(2, 2)-A(1, 2)-A(2, 1)$
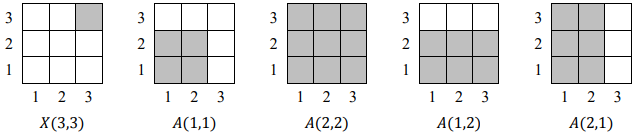
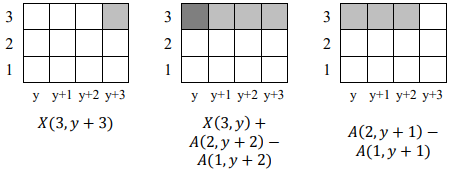
If for some $y$ ~y~ we know the value of $X(3, y)$ ~X(3, y)~, we can calculate $X(3, y+3)$ ~X(3, y+3)~: $X(3, y+3) = X(3, y)+A(2, y+2)-A(1, y+2)-(A(2, y+1)-A(1, y+1))$ .

Therefore we can calculate values of $X(3, 3)$ ~X(3, 3)~, $X(3, 6)$ ~X(3, 6)~, $X(3, 9)$ ~X(3, 9)~ and so on. Similarly we can calculate the values from the other end: $X(3, M-2)$ ~X(3, M-2)~, $X(3, M-5)$ ~X(3, M-5)~, $X(3, M-8)$ ~X(3, M-8)~ and so on. Now one of these two conditions holds:

$M \not\equiv 2 \pmod 3$ ~M \not\equiv 2 \pmod 3~. In this case either $X(3, 1)$ ~X(3, 1)~ or $X(3, 2)$ ~X(3, 2)~ will be known. It is easy to see that if the values of two out of three consecutive cells $X(3, k)$ ~X(3, k)~, $X(3, k+1)$ ~X(3, k+1)~, $X(3, k+2)$ ~X(3, k+2)~ are known, we can easily calculate the value of the unknown cell because the sum of all three cells equals $A(2, k+1)-A(1, k+1)$ ~A(2, k+1)-A(1, k+1)~. Therefore we can find all three values $X(3, 1)$ ~X(3, 1)~, $X(3, 2)$ ~X(3, 2)~ and $X(3, 3)$ ~X(3, 3)~ and then, moving from left to right, calculate values for the entire third row.
$M \equiv 2 \pmod 3$ ~M \equiv 2 \pmod 3~. In this case we will only know the values of $X(3, 3), X(3, 6), \dots, X(3, M-2)$ ~X(3, 3), X(3, 6), \dots, X(3, M-2)~. Let's consider the values of some three consecutive cells $X(3, k)$ ~X(3, k)~, $X(3, k+1)$ ~X(3, k+1)~ and $X(3, k+2)$ ~X(3, k+2)~. Exactly one of these three values is known and, as we established before, the sum of all three values is known as well. So the sum of two other values is known and we will denote it by $v$ ~v~. 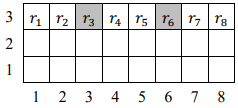For example, in the grid below, the sum of values can be calculated for the following pairs of cells: $\{r_1, r_2\}, \{r_2, r_4\}, \{r_4, r_5\}, \{r_5, r_7\}, \{r_7, r_8\}$ . What can this sum be? If $v = 0$ ~v = 0~ then it is clear that both values are $0$ ~0~. Similarly, if $v = 2$ ~v = 2~ then both values are $1$ ~1~. In these cases we know the values of three consecutive cells and we can then easily find the entire third row (as described in case 1). If, however, the sum of two cell values equals $1$ ~1~, it is unclear which of the values is $0$ ~0~ and which is $1$ ~1~. So, if for some three consecutive cells $v = 0$ ~v = 0~ or $v = 2$ ~v = 2~, we can find the entire third row. The only "bad" case is when for every three consecutive cells $v = 1$ ~v = 1~. In fact, this is not really a bad case. Observe that any $A$ ~A~ value which in its sum includes some unknown cell from the third row, includes exactly two unknown cells from the third row, and the sum of these two cells is known (and is equal to $1$ ~1~). It means that we don't care about the exact locations of the mines on the third row in these unknown cells and, if we consider them consecutively, there are two valid sequences: either $101010\dots$ ~101010\dots~ or $010101\dots$ ~010101\dots~. We can choose any of these two sequences (the solution is not unique in this case).

The grid of size $1 \times M$ ~1 \times M~

Positions of the mines are determined exactly the same way we found the third row. We will use notations $A(y)$ ~A(y)~ meaning $A(1, y)$ ~A(1, y)~ and $X(y)$ ~X(y)~ meaning $X(1, y)$ ~X(1, y)~:

First we find $X(3) = A(2)-A(1)$ ~X(3) = A(2)-A(1)~.
Then we find $X(6) = X(3)+A(5)-A(4)$ ~X(6) = X(3)+A(5)-A(4)~, $X(9)$ ~X(9)~, $X(12)$ ~X(12)~ and so on.
From the other end we find $X(M-2)$ ~X(M-2)~, $X(M-5)$ ~X(M-5)~, $X(M-8)$ ~X(M-8)~ and so on.
We find the entire row (in a way described before).

Finally, the solution of the original task (complexity is $\mathcal O(NM)$ ~\mathcal O(NM)~)

The solution consists of these steps:

First we find mine locations in the third row of the grid. Then in the same way we can find the sixth row, then the ninth row and so on.
In the opposite direction (from top to bottom) we find the rows $N-2$ ~N-2~, $N-5$ ~N-5~, $N-8$ ~N-8~ and so on.
Assuming that $N \not\equiv 2 \pmod 3$ ~N \not\equiv 2 \pmod 3~, the unknown rows will be either $1, 4, 7, 10, \dots$ ~1, 4, 7, 10, \dots~ (when $N \equiv 1 \pmod 3$ ~N \equiv 1 \pmod 3~) or $2, 5, 8, 11, \dots$ ~2, 5, 8, 11, \dots~ (when $N \equiv 0 \pmod 3$ ~N \equiv 0 \pmod 3~).
Since the unknown rows are apart from each other at a distance of $3$ ~3~, for each of them we can find mine locations independently, solving the $1 \times M$ ~1 \times M~ subtask.