From the task description, we know that the top left vertex of the plate is connected to the power source. The only other vertex in the top left tile that can be connected to the power is the opposite of that one. Observe that all the vertices that are opposite to those that can be connected to the power can also be connected to the power. We can continue in a similar way and identify all the vertices that can be connected to the power. Note that each tile has only two such vertices.

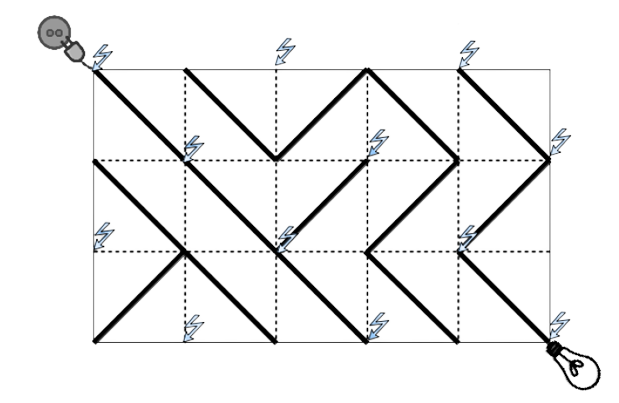
Let us construct a weighted graph. Let there be an edge between every pair of vertices belonging to the same tile. The edge has ~0~ weight if the wire on the tile matches the edge, or ~1~ otherwise. The weight ~1~ is chosen to indicate that the tile would have to be turned for the power to flow through its wire.

Now the solution is the shortest path from the power source to the lamp. This is best done with a 0-1 BFS, but due to the relatively small bounds, other shortest path algorithms will pass as well.