Editorial for Baltic OI '11 P8 - Tree Mirroring
Submitting an official solution before solving the problem yourself is a bannable offence.
The problem can be split into two parts:
- Find the leaves of the potential trees
and
(the vertices on the mirror plane).
- Recreate the trees and verify that they are equal.
The first part is the most difficult. To achieve that in time, one can use the following algorithm:
- Find any cycle
in
.
- If the edges of
are removed from
, the connected components of the remaining graph are either single vertices or they contain exactly two of the vertices in
, and these two are mirror images of each other in the tree-mirrored graph (if
is such graph). To find such a pair one can simply traverse this modified graph starting from any of the (non-isolated) vertices of
until another vertex of
is found.
- In the original graph, do separate breadth-first searches starting from these two vertices. Any vertex that appears at the same distance from both starting vertices is a potential leaf.
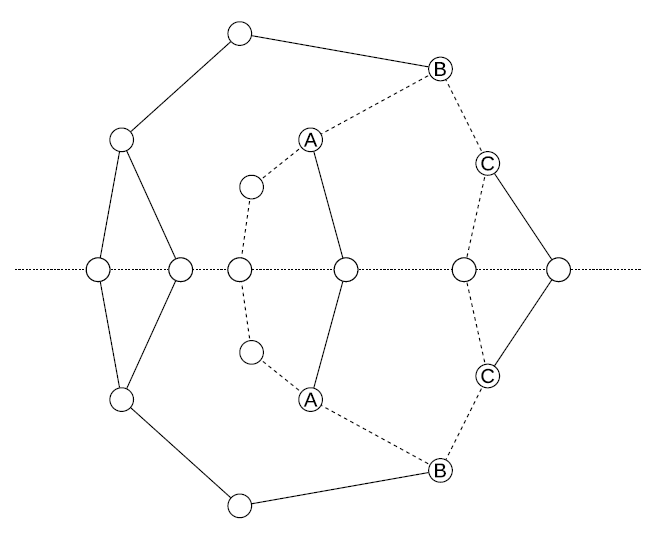
The second part can also be done in linear time. First, we divide the non-leaf vertices into the potential and
trees by traversing the graph with the leaves removed (check for cycles that would make
and
invalid trees). Now we construct a mapping between the vertices in
and
, for example by making a BFS starting from all leaves and identifying vertices that have the same corresponding child in the two trees. If no conflicts occur, the trees are identical.
There are also some special cases to keep track of. For example, if the graph contains two vertices with degree
these should directly be used as mirror images (if the number of such vertices is not zero or two we can say
NO directly). Moreover, if the graph is a single cycle, we just answer YES if and only if is even.
For partial scores, the problem can also be solved in time. For each vertex
with degree
, we simply assume that
is a leaf node and thus its two adjacent vertices are mirror images of each other and can be used to find all the leaves as above. For each such potential set of leaves, we then perform the second part of the solution.
Comments