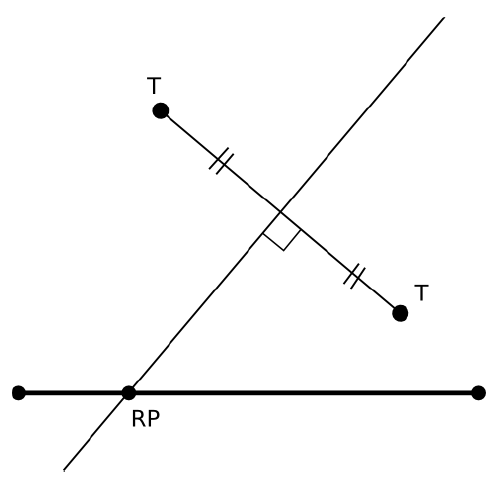
You can get a very easy solution by noticing that the only relevant points of the highway are its endpoints and the intersections with the perpendicular bisectors of the line segments that connect pairs of distinct transceiver stations. Location of these points is

$$\displaystyle 0.5\left(x_1 + x_2 + \frac{y_1^2 - y_2^2}{x_1-x_2}\right).$$

You can now calculate the distance from each of these points to the nearest transceiver. This solution takes ~\mathcal O(N^3)~ time.

With some optimizations for finding the nearest station, you can improve the performance to ~\mathcal O(N^2 \log N)~.

DP solution that checks all distinct pairs of transceivers takes ~\mathcal O(N^2)~ time.

A better solution is to do a binary search for the maximum distance of a point on the highway to the nearest transceiver station. You will need ~N~ to check, if some fixed distance will cover the entire road. So this solution will take ~\mathcal O(N \log M)~, where ~M~ is the maximum coordinate of a point.

The best solution is the following: using a stack, you go through the transceivers from left to right. You pop one element from it, if you can verify that it cannot be the closet station for any point on the road. The sorting in the beginning takes ~\mathcal O(N \log N)~, but if the input is already sorted, you can achieve ~\mathcal O(N)~.