First we can see that there is no difference between positive and negative ~y~ values, so all intersections ~(x, y)~ we can transform to ~(x, |y|)~. If we have to calculate minimal distance that citizen has to walk from single intersection then it depends from firework and intersection location:

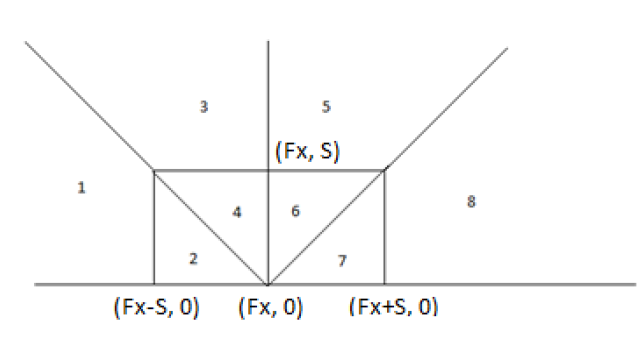
If fireworks is in point ~(F_x, F_y)~ ~(F_y = 0)~ and a citizen lives in intersection with coordinates ~(x, y)~, then if ~(x, y)~ is in region

1. citizen must walk distance ~y~.
2. ~y + S - (F_x - x)~
3. ~F_x - x~
4. ~F_x - x + S - y~
5. ~x - F_x~
6. ~x - F_x + S - y~
7. ~y + S - (x - F_x)~
8. ~y~

So if we have fixed firework position then all that is needed to calculate total distance for multiple intersections simultaneously are (for each region):

• Number of citizens in this region;
• Sum of x coordinates;
• Sum of y coordinates.

Which firework positions can give minimal total distance? As all distance functions are linear (while point do not change its region) then sum is also linear function therefore total function minimum (or one of them) will be when one of citizen house location is positioned on border between different regions. We can create all events (there are ~\mathcal O(n)~ events) when citizen house location cross any border, sort these events and use sweep line technique to process all events - each event require to calculate function value in this point (~\mathcal O(1)~ on each event) and update point that caused event region. Total complexity ~\mathcal O(n \log n~) because we have to sort all events and sweep line phase is ~\mathcal O(n)~.