Baltic Olympiad in Informatics: 2012 Day 2, Problem 3

Elder people still remember the famous computer game "TETRIS" created by Alexey Pajitnov, where pieces consisting of four squares (tetrominoes) fall from the sky and the goal of the game is to rotate and land every piece in a rectangular container creating as many lines of blocks without gaps as possible. When such lines are created, they disappear giving more space for the following pieces. Let's investigate a simpler version of the game, called "Tiny TETRIS" (or just "Tiny" for short). There are only nine different Tiny pieces (or t-pieces) consisting of one to three squares:

The number denotes the type of a t-piece and will be used further to reference the particular t-piece. The goal of the game is the same - falling t-pieces must be put in a rectangular container which is ~9~ units wide and ~9~ units high. Contrary to TETRIS, t-pieces cannot be rotated. Moreover, they cannot be moved to the left or right after they start falling. Thus, for each t-piece the player must only choose the container's column number (integer from ~1~ to ~9~) where the leftmost square of the piece (marked as ~\times~) will fall.

Each game consists of a finite sequence of ~N~ t-pieces from which as many as possible must be dropped in the container without exceeding its upper level or making an illegal move. The score of the game is equal to the number of successfully dropped t-pieces. At the beginning the game counter is set to ~0~. The algorithm of the game is the following:

1. Player chooses the column for the leftmost square of the current t-piece;
2. If the column is set correctly (for example, column ~8~ can never be correct for the t-piece ~5~), t-piece falls down until it meets an obstacle; otherwise the game is over.
3. If the t-piece fully fits inside the container (i.e., all squares are inside the ~9 \times 9~ rectangle) the value of the counter is increased by one. Otherwise, the game is over.
4. Then it is checked whether there are any completed horizontal lines (horizontal lines filled completely with blocks of t-pieces without any gaps). If there are any then these lines disappear and the lines above them are shifted down without changing their configuration.
5. If there are any t-pieces left, proceed to step ~1~. Otherwise the game is over.

The score of a particular game is the value of the counter at the moment when the game ends. Let's analyze one particular game.

Sequence of the given ~20~ t-pieces is the following: ~5,4,1,6,7,6,4,4,7,9,5,5,6,8,3,4,3,7,4,2~. Let's assume that the first ~17~ t-pieces have already been successfully dropped in the container in the columns ~1,2,2,4,8,8,7,4,8,6,1,1,4,8,3,7,7~, respectively. Until this moment no lines have been completed, the current value of the counter is ~17~ and it is time to drop t-piece ~7~ (letters in the figure are assigned consecutively to t-pieces):

There are only two valid columns where t-piece ~7~ can be dropped:

a) column ~1~:	b) column ~5~ (in this case one line will be completed and, therefore, disappear):

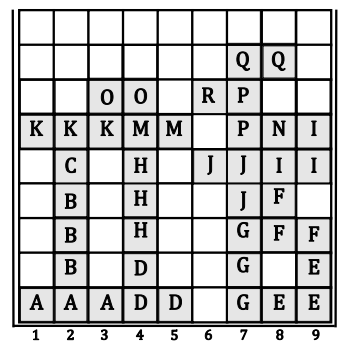Input Specification

The problem has been adapted from its original format for DMOJ. Your program is given five files each containing a description of a particular game: tiny.i1, tiny.i2, tiny.i3, tiny.i4, and tiny.i5. They can be downloaded here for you to study: tiny.zip. Each file contains the sequence of t-pieces and has the following format: the first line contains a single integer ~N~. The next ~N~ lines describe the t-piece sequence; each line contains an integer between ~1~ and ~9~ - the number of the particular t-piece. T-pieces are given in the order how they must be dropped in the container; the ~i~-th t-piece is given in the ~i+1~-st line of the file.

Output Specification

For each of the given input files, you must output at most ~N~ rows - the numbers of the columns where pieces are dropped. The ~i~-th row of the output file must contain the number of the column where the ~i~-th t-piece from the input data must be dropped.

It is guaranteed that for each input file there exists a sequence of columns which allows all t-pieces to be successfully dropped in the container (and gets the final score for the game equal to ~N~).

Grading

Each of the five test cases is worth ~2\,000~ points. The amount of points you will receive for a particular output file (test case) is calculated using the following formula:

$$\displaystyle 2\,000 \times \frac{\text{your score}}{N}$$

rounded to the nearest integer.