Editorial for Baltic OI '13 P3 - Pipes - DMOJ: Modern Online Judge

Editorial for Baltic OI '13 P3 - Pipes

Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.

Task

A connected, simple, graph on $n$ ~n~ vertices and $m$ ~m~ edges is given. Weights are assigned to all edges (they are integers but need not be positive). These weights are not known but for each vertex the sum of weights of the edges incident to it is given. Can the weights be determined uniquely? If yes, what are they?

Intended Solution

We will use graph theoretic terminology, seeing reservoirs as vertices and pipes as edges of a graph $G$ ~G~. For each edge $e$ ~e~, let $w_e$ ~w_e~ be its weight. We allow $w_e$ ~w_e~ to take integer values, with the following interpretation:

if $w_e \ge 0$ ~w_e \ge 0~ then $2w_e$ ~2w_e~ $m^3/s$ ~m^3/s~ of water is pumped into $e$ ~e~,
if $w_e \le 0$ ~w_e \le 0~ then $-2w_e$ ~-2w_e~ $m^3/s$ ~m^3/s~ of water is drained from $e$ ~e~.

For each vertex $v$ ~v~, we know

$\displaystyle s_v = \sum_{e \in \Gamma(v)} w_e \quad (1)$

which is the sum of weights of the edges incident to $v$ ~v~ ( $\Gamma(v)$ ~\Gamma(v)~ is the set of such edges). Note that $(1)$ ~(1)~ gives $n$ ~n~ linear equations for $m$ ~m~ unknowns $w_e$ ~w_e~. There can be a unique solution only if $m \le n$ ~m \le n~ (this is true even for integer values of $w_e$ ~w_e~) $(\star)$ ~(\star)~. Moreover, as $G$ ~G~ is connected, $m \ge n-1$ ~m \ge n-1~.

Suppose $m = n-1$ ~m = n-1~. Then $G$ ~G~ is a tree and has a leaf (a vertex of degree one, that is, with exactly one incident edge). Pick a leaf $v$ ~v~ and let $u$ ~u~ be the vertex to which $v$ ~v~ is joined by an edge. Then $(1)$ ~(1)~ gives $w_{uv} = s_v$ ~w_{uv} = s_v~ which is known. Remove $v$ ~v~ together with the edge $uv$ ~uv~ from $G$ ~G~ and subtract $w_{uv}$ ~w_{uv}~ from $s_u$ ~s_u~. The remaining graph is again a tree. Continue this process until a single vertex remains. Then $G$ ~G~ has a unique solution which we have found.

Now suppose $m = n$ ~m = n~. Remove leaves as before, until there are no more leaves. What remains is a connected graph on $n' = n-l$ ~n' = n-l~ vertices and $m' = n-l$ ~m' = n-l~ edges where $l$ ~l~ is the number of leaves removed. This is a cycle of length $n'$ ~n'~. If $n'$ ~n'~ is even then there are multiple solutions (see Fig. 1).

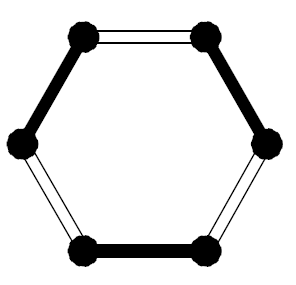
Figure 1: Cycles of even length have multiple solutions: given one solution, add one to black edges and subtract one from white edges to get another.

If $n'$ ~n'~ is odd, however, we have a unique solution. Indeed, suppose $1, 2, \dots, n'-1$ ~1, 2, \dots, n'-1~ are the vertices in this order. From $(1)$ ~(1)~ we have

$\displaystyle \begin{align*} w_{n'1} &= s_1 - w_{12} \\ &= s_1 - s_2 + w_{23} \\ &= s_1 - s_2 + s_3 - w_{34} \\ &\mspace{120mu} \vdots \\ &= s_1 - s_2 + s_3 - \dots + s_{n'} - w_{n'1} \end{align*}$

$\displaystyle w_{n'1} = \frac{s_1 - s_2 + s_3 - \dots + s_{n'}}{2}$

This determines $w_{n'1}$ ~w_{n'1}~ uniquely and having its value we can easily fill in the remaining weights: $w_{12} = s_1-w_{n'1}$ ~w_{12} = s_1-w_{n'1}~, $w_{23} = s_2-w_{12}$ ~w_{23} = s_2-w_{12}~ and so on.

If $m > n$ ~m > n~, we know from earlier considerations that there is more than one possible solution.

Given a connected graph $G$ ~G~ on $n$ ~n~ vertices, we can do this in total time $\mathcal O(n)$ ~\mathcal O(n)~: find the initial leaves of $G$ ~G~ and put them in a stack. Consider the top leaf: remove it and decrease the degree of its neighbour. Check if this degree is one: if yes, add the neighbour to the stack. Do this until no leaves remain. So the total time complexity is $\mathcal O(n)$ ~\mathcal O(n)~.

Remark

Observation $(\star)$ ~(\star)~ can be made purely by combinatorial considerations without using any linear algebra. If $G$ ~G~ is connected on $n$ ~n~ vertices and at least $n+1$ ~n+1~ edges then it contains at least two cycles. If one of them has even length, there cannot be a unique solution (Fig. 1). Assume they both have odd length. There are two cases.

The cycles have at most one vertex in common. As $G$ ~G~ is connected, there is a path $p$ ~p~ that joins the cycles (we allow $p$ ~p~ to be a single vertex). In Fig. 2, on the left is the case when $p$ ~p~ has even length (that is, $p$ ~p~ has an even number of edges) and on the right is the case when $p$ ~p~ has odd length. In both cases, there is more than one solution.

Figure 2: Perturb weights to get a new solution.

The cycles share at least two vertices. Let $x$ ~x~ be one of the common vertices. Start at $x$ ~x~ and follow one of the cycles until it intersects the other cycle. Let this intersection point be $y$ ~y~. There are three paths joining $x$ ~x~ and $y$ ~y~, any pair of which intersect only at endpoints (see Fig. 3. Let $l_1$ ~l_1~, $l_2$ ~l_2~ and $l_3$ ~l_3~ be their lengths. Pairs of these paths form cycles of lengths $l_1+l_2$ ~l_1+l_2~, $l_2+l_3$ ~l_2+l_3~ and $l_3+l_1$ ~l_3+l_1~. At least one of these numbers is even so there is a path of even length. Referring back to Fig. 1, we know there cannot be a unique solution.

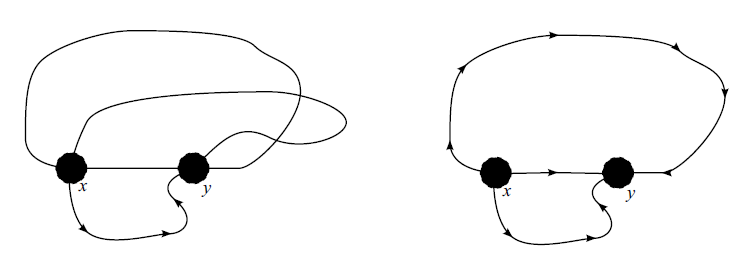
Figure 3: Three pairwise disjoint paths join $x$ to $y$ . We must have an even cycle.

Comments

There are no comments at the moment.