Let  denote the number of calls Wotan needs to end the game when
denote the number of calls Wotan needs to end the game when  children are left and let
children are left and let  be the set of primes Wotan can choose from.
be the set of primes Wotan can choose from.
Dynamic Programming Solution
For  points it is enough to evaluate the obvious formula
points it is enough to evaluate the obvious formula

using dynamic programming. Then all queries can be answered by simple lookup. To handle the case  suffices to check whether
suffices to check whether

(since if  is not divisible by
is not divisible by  after calling
after calling  less children will be over, but if
less children will be over, but if  is at least the product
is at least the product  of all numbers Wotan can call, after any call at least
of all numbers Wotan can call, after any call at least  children will remain) or to simply set
children will remain) or to simply set  for
for  before evaluating the above formula. Runtime is
before evaluating the above formula. Runtime is  in both cases.
in both cases.
Greedy Approach
Let us denote the predecessor, i.e. the number of children that are left after Wotan made a perfect call, of  as
as  ). If there are multiple solutions, let
). If there are multiple solutions, let  be the minimum of these numbers. The main point of the solution is the following
be the minimum of these numbers. The main point of the solution is the following
Proposition 1. Wotan can call the numbers greedily, i.e.  . This fact is—once stated—quite obvious, but it can be established rigorously using the following
. This fact is—once stated—quite obvious, but it can be established rigorously using the following
Lemma 2.  and
and  are both monotonically increasing in
are both monotonically increasing in  .
.
Proof. We show this for any interval ![[0 \dots N]](//static.dmoj.ca/mathoid/69f7561cb7669bb3e894748cefd3f48e9d2ad310/svg) by induction on
by induction on  . Without loss of generality let us assume that
. Without loss of generality let us assume that  . The case
. The case  is trivial. Otherwise we have
is trivial. Otherwise we have  as stated above and thus
as stated above and thus  . Since
. Since  for any
for any  ,
,  we have
we have  . Thus
. Thus

because of the monotonicity of  in
in ![[0 \dots \pi(N)] \subseteq [0 \dots N-1]](//static.dmoj.ca/mathoid/942de8bd45e91f006a4c27f31dc4ca94fd329454/svg) .
.
To show that this suffices for subtask  we need to establish an upper bound for
we need to establish an upper bound for  . For simplicity let
. For simplicity let  denote
denote  .
.
Lemma 3. Let  and
and  . Then
. Then  .
.
Proof. We use induction on  . Again there is nothing to show for
. Again there is nothing to show for  . For
. For  we have
we have  by assumption and thus
by assumption and thus

by monotonicity of  . Using the monotonicity of
. Using the monotonicity of  we get thus
we get thus  .
.
Once again using monotonicity we get
Corollary 4. If  , then
, then  . Especially we have
. Especially we have  .
.
Using the prime number theorem stating that the  prime is asymptotically as big as
prime is asymptotically as big as  one can decrease this bound further to
one can decrease this bound further to  , however, this is not required directly for the solution.
, however, this is not required directly for the solution.
Since we can calculate  primitively in
primitively in  we can answer one query in
we can answer one query in  time. This suffices for subtasks
time. This suffices for subtasks  and
and  .
.
DP Over Inverse Function
Let  denote the inverse function of
denote the inverse function of  , i.e.
, i.e.

Since  and thus
and thus  , we have
, we have

Thus having calculated  for
for ![x \in [1 \dots k]](//static.dmoj.ca/mathoid/ebc0e5d1ba21007d9f69a0293fc2d9b6195a17ba/svg) one can calculate
one can calculate  using binary search in the interval
using binary search in the interval ![[d^{(-1)}(k), d^{(-1)}(k)+k_{\max}]](//static.dmoj.ca/mathoid/c1b2a0ac0e2a88e002d9b4f6988cef05ccf101c6/svg) . It further suffices to check for given
. It further suffices to check for given  in this interval whether
in this interval whether  (instead of really calculating
(instead of really calculating  , which would be too slow). So one can calculate this function for every needed value of
, which would be too slow). So one can calculate this function for every needed value of  in time
in time  (here the additional log-factor mentioned before comes in handy).
(here the additional log-factor mentioned before comes in handy).
With this function one can answer any query in logarithmic time using binary search or simply fill an array ![d[1 \dots n]](//static.dmoj.ca/mathoid/1110c1ef110369390c9b996e6c39204689029a1e/svg) of all values in time
of all values in time  and then answer queries in
and then answer queries in  . Both suffices to get full score.
. Both suffices to get full score.
Model Solution: Fast Evaluation of the Predecessor Function
Instead of minimizing  we can simply maximize the term we subtract (since
we can simply maximize the term we subtract (since  is fixed), let's call it
is fixed), let's call it  . If we plot some of those functions for variable
. If we plot some of those functions for variable  and some
and some  the image consists of a set of straight lines of slope
the image consists of a set of straight lines of slope  and "breaks".
and "breaks".
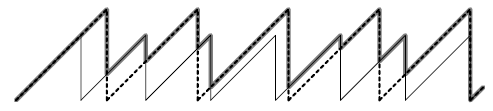
Thus for  we get the same simple characteristic. If we plot all those functions — both
we get the same simple characteristic. If we plot all those functions — both  and
and  — and scan through this image from right to left the optimal
— and scan through this image from right to left the optimal  can only change when a break occurs. Thus if we evaluate
can only change when a break occurs. Thus if we evaluate  at all those breaks of all the
at all those breaks of all the  -functions we can simply fill in the rest of them by subtracting one from the next one at the right.
-functions we can simply fill in the rest of them by subtracting one from the next one at the right.
For any breakpoint  , we have that
, we have that  is
is  for some
for some  . Thus to initialize our array
. Thus to initialize our array ![M[1 \dots n]](//static.dmoj.ca/mathoid/0c2437ddb4d13c35a91f511a77974de1a9c7605f/svg) of values of
of values of  it suffices to set
it suffices to set ![M[ak-1] = k-1](//static.dmoj.ca/mathoid/3cde758c6769a1e83c2e409fbc5c63706a8d4b41/svg) for any
for any  and increasing
and increasing  . This needs
. This needs

steps (messing with analytic number theory one can reduce this bound further to  but with really good constant factor.
but with really good constant factor.
Afterwards one can calculate  on the fly in constant time and thus use the simple DP approach from the beginning to get full score.
on the fly in constant time and thus use the simple DP approach from the beginning to get full score.
An implementation using a priority queue to evaluate  using the same ideas above is expected to get something around full score, too, depending on the data structure used.
using the same ideas above is expected to get something around full score, too, depending on the data structure used.

Comments