Strangely enough, there's been a break-in at the company headquarters!
Unfortunately, the lack of security cameras in the building means that the criminal(s?) will escape scot-free.

To prevent such a thing from happening again, the company has decided to purchase some security cameras.
To simplify things a bit, we'll assume the building is very simple - the various passages in the company can only go north/south or east/west.
Now, these cameras contain mirrors that allow them to have a fairly good field of view.
Because of distortion and other factors, though, they can only see "straight" (see diagram).
The company would like to place cameras so that each hallway is completely covered by one (or more) cameras.
These cameras are expensive, of course, and so you'd like to minimize the number of cameras required.

Input Specification

~N \le 100~, the number of hallways.
For each hallway, ~1~ line:
~4~ integers ~x_1, y_1, x_2, y_2~, representing the start and end locations of the hallway respectively.
Assume the company floor is a 2D plane with ~(0,0)~ being the southwest corner and ~(10\,000, 10\,000)~ the northeast corner.
Each hallway will either have ~x_1 = x_2~ or ~y_1 = y_2~ (not both!).
Parallel hallways will never overlap.

Output Specification

The minimum number of cameras required.

Sample Input

6
1 4 7 4
2 2 2 4
2 2 6 2
6 1 6 6
5 1 6 1
3 6 5 6

Sample Output

4

Diagram

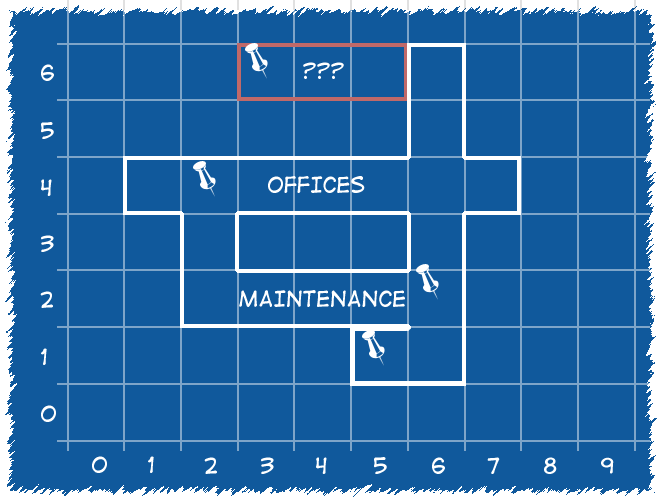
By putting cameras in the locations, uh, shown, every building location is covered.