Canadian Computing Competition: 2005 Stage 2, Day 1, Problem 3

You have a grid with one distinguished location at some unknown position ~(X, Y)~. The bottom left corner of the grid is ~(0, 0)~.

Not all the grid positions are eligible to contain the distinguished location. A polygon is marked on the grid. This polygon indicates the possible locations for the distinguished location. The polygon is closed, has no interior holes, and is convex. It also has the property that every edge of the polygon runs in one of the eight directions ~N, S, E, W, NW, SE, NE, SW~.

Recall that a polygon is convex when it contains (encloses) all the line segments connecting any pair of its points. Luckily for you, the Oracle knows where the distinguished point is. You are trying to identify the distinguished location by asking questions of the Oracle.

Each question consists of: "I'm thinking of a line running ~N~ or ~S~, ~E~ or ~W~, ~NW~ or ~SE~, ~NE~ or ~SW~ through location ~(x, y)~."

Each question is answered by: "The distinguished point is to the left, right, or on the line."

Constraints

~0 \le X < N \le 11~

~0 \le Y < M \le 11~

Interaction

The first line of input contains the two integers ~N~ and ~M~, indicating the width and height of the grid. The next ~M~ lines consist of ~N~ characters, either . or X. The X positions are eligible to contain the unknown position ~(X, Y)~.

You will then start the interaction by proceeding with your questions to the Oracle. Each question should be formatted as ? x y d, with ~0 \le x < N~ and ~0 \le y < M~. The third integer can be one of four integers, where:

• ~d = 1~ corresponds to a vertical line (slope of ~\infty~) through the point ~(x, y)~
• ~d = 2~ corresponds to a line going ~NE~ or ~SW~ (slope of ~1~) through the point ~(x, y)~
• ~d = 3~ corresponds to a horizontal line (slope of ~0~) through the point ~(x, y)~
• ~d = 4~ corresponds to a line going ~NW~ or ~SE~ (slope of ~1~) through the point ~(x, y)~

The Oracle returns one of three integer values:

• ~-1~ if the point is to the left of the line
• ~0~ if the point is on the line
• ~1~ if the point is to the right of the line

For each case, the diagram below should explain what is meant by left and right:

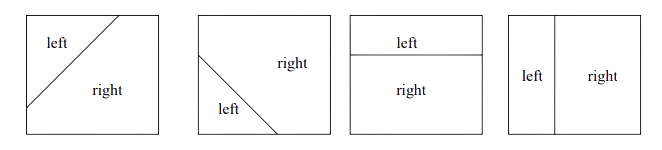
When you believe you have found the unknown point ~(X, Y)~, output ! X Y. Your program should ask as few questions as possible (note: if you query more than ~22~ times, your program will receive -2 and the interactor will terminate) to the Oracle until you are certain of the distinguished location. That is, you should minimize the maximum possible number of questions asked, regardless of the distinguished location.

If at any point your question breaks constraints, your program will receive -2 and the interactor will terminate. Upon receiving -2, your program should terminate to avoid an undefined verdict.

Please note that you may need to flush stdout after each operation, or interaction may halt. In C++, this can be done with fflush(stdout) or cout << flush (depending on whether you use printf or cout). In Java, this can be done with System.out.flush(). In Python, you can use sys.stdout.flush().

Sample Interaction

>>> denotes your output. Do not print this out.

10 10
......X...
.....XXX..
....XXXXX.
...XXXXXXX
..XXXXXXXX
.XXXXXXXX.
XXXXXXXX..
.XXXXXX..
..XXXX...
...XX....
>>> ? 5 5 1
-1
>>> ? 2 5 3
-1
>>> ? 2 6 3
0
>>> ? 4 6 1
0
>>> ! 4 6