Definition 1. A portal is a straight line connecting two trees. A point ~p~ is called allowed if you can see all trees from it. A path is allowed (or valid), if all of its points are allowed. If a point is not allowed, we call it forbidden, and likewise for paths.

The main point of our solution is that for any camp, we only need to check two paths. The proof will consist of several steps.

Remark 2. If ~a~ is reachable from ~b~ (meaning there is a valid path connecting them), then this is still possible if we restrict ourselves to piecewise linear paths that only bend on portals.

Proof. First note that the set of forbidden points is given as follows: for any pair ~(s, t)~ of trees, we have a "forbidden ray" going out of ~t~ with direction ~t-s~ (these are precisely the points where you can't see ~s~ because of ~t~). Thus if we remove forbidden points and all the portals, we get the plane with some lines removed, which splits into convex regions. Thus any two points on portals bounding the same region can be connected by a straight line of allowed points. □

The most important result is the following:

Lemma 3. If ~b~ is reachable from ~a~ and at least one of them lies on a portal, then the segment ~\overline{ab}~ is valid.

Proof. W.l.o.g. assume that ~b~ lies on a portal and let ~\gamma~ be a valid piecewise linear path connecting ~a~ and ~b~ which has ~n~ bend points. We can restrict ourselves to the case ~n = 1~: for ~n = 0~, there is nothing to show and the general case follows easily by induction.

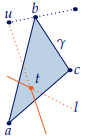
Let ~c~ be the bend point and consider the triangle ~\Delta~ formed by ~a~, ~b~, and ~c~. Assume that ~\overline{ab}~ would be forbidden, i.e. there is a forbidden ray intersecting ~\overline{ab}~. Let ~l~ be the respective line. Since ~l~ would intersect one of the other two sides, there must be a tree ~t~ inside ~\Delta~. Now take one tree ~u~ of the portal which is not on the same side of ~\overline{ab}~ as ~t~. Then ~ut~ intersects ~\overline{ab}~ and thus another side of ~\Delta~. At this intersection point, ~u~ is hidden by ~t~ and so it is forbidden, which contradicts the choice of ~\gamma~. □

Fix a portal. If we remove all the forbidden points from this portal, it splits into a set ~S~ of segments. Obviously, for any ~s \in S~, either all points are reachable or none. Applying the previous lemma, we see that a segment is reachable if and only if the midpoint is reachable via a direct line.

Hence we can give an ~\mathcal O(N^6 C)~ algorithm, which scores 20 points, as follows: for any of the ~\mathcal O(N^2)~ portals calculate all intersections with the ~\mathcal O(N^2)~ forbidden rays. This gives up to ~\mathcal O(N^4)~ segments. Then for a fixed camp and any segment, check if we can reach the midpoint from both the camp and Gimli via a direct line, which needs ~\mathcal O(N^2)~ intersection checks per midpoint. Finally, check the direct line from Gimli to the camp itself.

For any polygon ~P~, we denote by ~\partial P~ its border. The following result allows us to optimise the above algorithm:

Remark 4. Let ~F~ denote the forest (as in the task statement) and let ~\Gamma~ be the convex hull of the trees. As above, let ~a~ and ~b~ be arbitrary points in ~F~. If ~b~ lies on ~\partial F~ and is reachable from ~a~, then it is already reachable either via a direct line or via a piecewise linear path having its only bend point on ~\partial \Gamma~.

Proof. Let ~\gamma~ be an allowed path from ~a~ to ~b~ that bends only on portals. If ~\gamma~ intersects ~\partial \Gamma~ this follows as above. Otherwise, since ~b~ is not contained in the interior of ~\Gamma~, the whole path must lie outside ~\Gamma~ and thus cannot intersect any portal. Hence, by construction, ~\gamma~ is a segment. □

In ~\mathcal O(N^4)~, we can calculate all intersections between ~\partial \Gamma~ and forbidden rays. By convexity, any ray can intersect ~\partial \Gamma~ in at most ~1~ point, hence there are only ~\mathcal O(N^2)~ segments to consider. Thus the obvious modification of the above algorithm has runtime ~\mathcal O(N^4 C)~, which gets another 20 points (10 points from the convex subtask).

If all trees lie on ~\partial \Gamma~, then all forbidden points (except the trees) are outside ~\Gamma~ and hence you only need to look at midpoints of portals on ~\partial \Gamma~. This gives an ~\mathcal O(N^3 C)~ algorithm which scores 20 points, or when combined with the above solution, 50 points.

For 80 points, you need the following observation:

Definition 5. Fix a tree ~t~. The forbidden rays beginning at ~t~ split the plane into different regions, exactly one of which contains Gimli's original position. The two rays bounding this region and their points are called strictly forbidden.

Remark 6. A path ~\gamma~ beginning at Gimli's original position is allowed if and only if it contains no strictly forbidden points.

Proof. The "only if" part is trivial. Now let ~p~ be a forbidden point, that is not strictly forbidden, and ~t~ the respective tree. Then by definition, ~\gamma~ must cross one of the forbidden rays beginning at ~t~ in order to reach ~p~, i.e. it must contain a strictly forbidden point. □

The forbidden rays can be easily found in ~\mathcal O(N^2)~. From this, we can get an ~\mathcal O(N^2 C)~ solution by applying the above procedure only to the strictly forbidden rays: all the midpoints omitted are anyhow not reachable from Gimli.

For full score, you can use the following final result:

Remark 7. Let ~a~ and ~b~ be points on (possibly distinct) portals, that are both reachable from Gimli, and let ~c~ be an arbitrary point. Then the segment ~\overline{ac}~ is allowed if and only if ~\overline{ab}~ is valid.

Proof. Note that you can get from ~a~ to ~b~ and vice versa (simply by composing the paths to Gimli's original position). Thus ~c~ is reachable from ~a~ iff it is reachable from ~b~. So the claim follows from Lemma 3. □

So we can solve the problem in ~\mathcal O(N^2 + NC)~ as follows: calculate the forbidden rays as above and then in ~\mathcal O(N^2)~ the reachable segments on ~\partial \Gamma~. Then for any camp ~c~, check both the direct line from Gimli's original position to ~c~ and, if it exists, the direct line from an arbitrary reachable midpoint to ~c~.

Some further notes

The proof of our main lemma only requires that there are trees on either side of ~ab~. As you can see from the practice task "surveyor", this holds if either ~a~ or ~b~ is contained in the convex hull ~\Gamma~. Thus, we do not need the restriction that all the camps are located on ~\partial F~: any point inside ~\Gamma~ is reachable via a direct line, and for Remark 4, we only require ~b~ to be outside ~\Gamma~. Hence the above algorithm also works in general.

After ~\mathcal O(N^2)~ preprocessing time, we only need to check for up to two points which camps are reachable via a direct line. This could be also done in ~\mathcal O((N+C) \log(N+C))~ by sweeping over angles.

The following proposition offers an easier to implement solution.

Proposition 8. For any tree ~t~, removing the strictly forbidden points (including ~t~) splits the plane into two parts, exactly one of which contains Gimli's original position. Call this region ~G_t~. Then a camp ~c~ is reachable from Gimli if and only if it is contained in ~G_t~ for all trees ~t~.

Proof. Obviously, every point reachable from Gimli's original position lies in the intersection of all ~G_t~. It remains to show that the intersection of all regions ~G_t~ is connected.

If the tree ~t~ lies inside the convex hull ~\Gamma~ of the forest, the region ~G_t~ is the intersection of two half-planes (in particular convex). On the other hand, this need not be the case if ~t~ is a corner of the convex hull. But if ~G_t~ is non-convex, it is easy to see that ~G_t~ at least contains all other trees (cf. Figure 1).

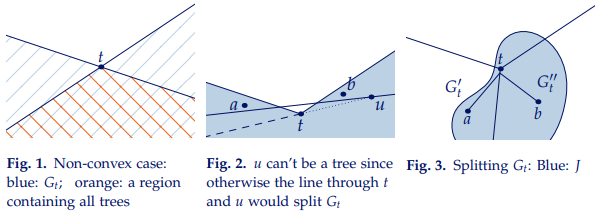
We are now going to show that for any subset of the set of non-convex regions ~G_t~ and any set of half-planes through trees, the intersection of these non-convex regions and half-planes is connected. This is obviously sufficient to prove the claim, as it implies that the intersection of all regions ~G_t~ is connected. We are going to use induction on the number of non-convex regions we consider. The intersection of half-planes is convex and thus connected, so we may assume that there is at least one such non-convex region ~G_t~. Let ~J~ be the intersection of the half-planes and the other non-convex regions. By drawing a picture, you can easily see that ~J \cap G_t~ lies completely within a half-plane through the tree ~t~ contained in ~G_t~ or ~t~ is contained in (or on the border of) ~J~ (since ~t~ lies in all non-convex regions ~G_u~ and lines through trees cannot divide ~t~ from both ~a~ and ~b~, cf. Figure 2).

In the first case, simply apply the induction hypothesis (replacing the non-convex region ~G_t~ by the half-plane through ~t~). In the second case, split ~G_t~ into two convex regions ~G'_t~ and ~G''_t~ using a line through ~t~. Both regions are the intersection of two half-planes through ~t~, so by induction, the sets ~J \cap G'_t~ and ~J \cap G''_t~ are both connected. Furthermore, ~t~ is contained in (or on the border of) ~J \cap G'_t~ and ~J \cap G''_t~. But that means that the union ~(J \cap G'_t) \cup (J \cap G''_t) = J \cap G_t~ is connected (two points ~a \in J \cap G'_t~ and ~b \in J \cap G''_t~ are connected via a point close to ~t~, cf. Figure 3). □

Note that this relies heavily on the structure of the ~G_t~'s and is false for arbitrary sets. For example, you can take the sets ~A~ and ~B~ obtained by removing from the unit circle the points ~(0, 1)~ and ~(0, -1)~, respectively. Then both ~A~ and ~B~ contain paths from ~(-1, 0)~ to ~(1, 0)~, but their intersection doesn't.