CEOI '22 P4 - Drawing
View as PDFPaint & Wine is the first painting studio in Zagreb offering relaxing painting lessons with a glass of wine on the side. During the lesson, students are given a certain theme, and with the aid of master painters usually manage to paint an impressive piece.
Ante is a master painter, Luka is his student, and this task tells the tale of a lesson that included a bit more wine than usual.
Ante: "Paint me a tree!"
Luka: "Alright. What kind of tree do you want? Palm, oak, pine. . . ?"
Ante: "I want a connected acyclic undirected graph!"
Luka: "I can do that. . . Any other wishes?"
Ante: "I like it when no node is adjacent to more than three other nodes!"
Luka: "Uhm, okay. . .Well, there are many such trees."
Ante: "Here is a list of edges, I want that one!"
Luka: "Ok, wow. Still, there are many ways to draw it."
Ante: "Here is a list of points in the plane where I want the nodes to be drawn. I also don't want to see a pair of intersecting edges."
Luka: "I'm on it!"
Your task is to help Luka paint the tree according to Ante's wishes. More precisely, given a description of a tree, such that no node is adjacent to more than three other nodes, and a list of points in the plane, find a one-to-one mapping of nodes to points such that, when edges of the tree are drawn as line segments between corresponding points, they do not intersect (except at end points).
Input Specification
The first line of input contains an integer , the number of nodes in the tree and the number of points in
the plane.
The following lines describe edges of the tree, one per line. Each edge is described by two integers
and
, labels of nodes connected by the edge. Nodes are labelled with integers from
to
.
It is guaranteed that each node is adjacent to at most three other nodes.
The following lines contain the points to be used when drawing the tree, one per line. Each point is
described by a pair of integer coordinates. No two points share the same pair of coordinates, and no three points lie on the same line.
Output Specification
Output a permutation of integers from to
in a single line. The
-th number should be the label of the
node which is mapped to the
-th input point.
If there are multiple valid solutions, output any of them. It's guaranteed that a solution always exists.
Constraints
For all subtasks:
Point coordinates are integers between and
.
| Subtask | Score | Constraints |
|---|---|---|
Sample Input 1
3
1 2
2 3
10 10
10 20
20 10Sample Output 1
1 2 3Sample Input 2
5
1 2
1 3
1 4
4 5
10 10
10 30
30 10
30 30
20 25Sample Output 2
5 4 2 3 1Sample Input 3
6
1 2
2 3
1 4
4 5
4 6
10 60
10 40
40 50
40 30
70 30
70 10Sample Output 3
6 5 4 1 2 3Explanation for Sample 3
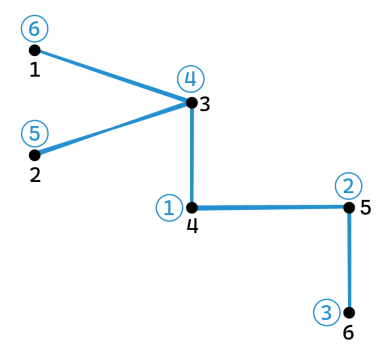
Blue numbers represent node labels while black numbers represent point indices.
Comments