CEOI '22 P5 - Measures
View as PDFThe COVID-19 pandemic took the world by surprise in many ways. Almost overnight, people around the globe had to adapt to a new way of life, mainly shaped by the preventive measures issued by their local authorities, all with the goal of suppressing and controlling the spread of the disease.
To better prepare for the unlikely event of a more devastating outbreak in the future, the Croatian National Institute of Public Health decided to open various research departments. The main goal of these departments is to develop highly efficient protocols that help the general population to quickly adhere to a new preventive measure.
Alenka works in one such department, and is currently investigating the scenario in which a group of people stands in a line, e.g. in front of a post office, and suddenly a new safety measure takes place, mandating the distance between any two people has to be at least .
She also implemented an app that allows the user to specify a distance and locations of
people as coordinates along a line. The app then draws a picture of a line which represents the situation, and calculates the smallest amount of time in seconds, denoted as topt, needed for the group to reach a new arrangement that satisfies the preventive measure. The app assumes that people are going to immediately start rearranging themselves optimally, and that all people move with the same constant speed of one unit per second.
She now wants to add a new feature that will enable the user to add additional people to the group by tapping on the drawn line, thereby specifying their locations. The app is supposed to recalculate
after each tap, i.e. after each new person is added to the group.
Your task is to help Alenka by implementing this feature.
Input Specification
The first line contains integers ,
, and
from the task description.
The second line contains integers
, the locations of the
initial people.
The third line contains integers
, the locations of the
additional people.
Output Specification
Output numbers in one line, the
-th of them representing the value of
given that the group consists of
people at locations
.
Output each number in decimal notation without trailing zeroes, e.g. output 1.23 instead of 1.2300, and 123 instead of 123. or 123.0. It can be proven that answers always have a finite decimal representation.
Constraints
For all subtasks:
| Subtask | Score | Constraints |
|---|---|---|
Sample Input 1
2 1 2
1 3
2Sample Output 1
1Sample Input 2
0 5 3
1 2 3 4 5Sample Output 2
0 1 2 3 4Explanation for Sample 2
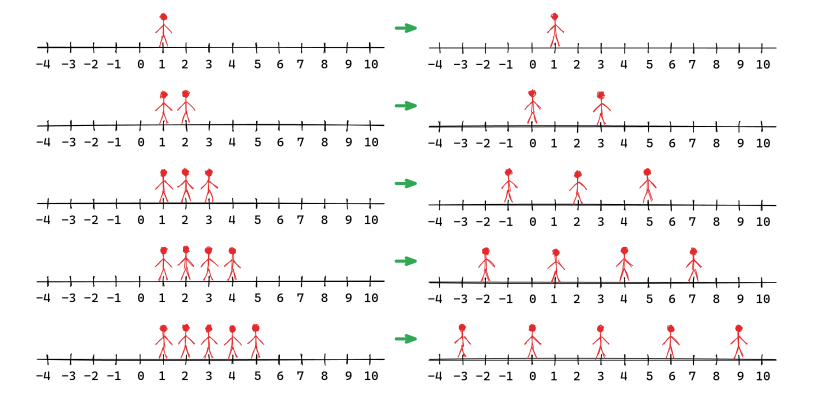
Sample Input 3
3 3 3
3 3 3
3 3 3Sample Output 3
4.5 6 7.5
Comments