Prepared by: Ivan Paljak and Krešimir Nežmah

The first subtask can be solved in various ways. Since ~M~ is small, it's possible to go over all the cases systematically with pen and paper. Alternatively, we can have a brute force solution which uses BFS to go over the state space.

If at any point there are two vehicles of the same color in the same parking spot, we can ignore this parking spot for the rest of the process since these vehicles are in the correct spot. If two vehicles of the same color are not initially in the same parking spot, then we obviously need to spend at least one move for this color. Additionally, if both of these vehicles are top vehicles, we clearly need at least two moves. As we'll see later, there is one more case where we have to use an additional move (one of the cycle cases). We will present a solution which constructs a sequence of moves that achieves this bound, in case a solution exists.

Each parking spot contains two positions (the bottom one and the top one). We'll create a graph with ~2M~ nodes representing the parking spot positions. The edges are defined as follows:

• if two vehicles of the same color are in different parking spots, we connect their positions,
• if a parking spot is full, we connect the bottom and the top position.

Each connected component of such a graph will be either a cycle, or a chain, where the ends of the chain are two bottom vehicles. If a connected component has two adjacent top nodes, we'll call such a pair a top pair for this connected component. Note that a top pair corresponds to two top vehicles of the same color in different parking spaces. We define the term bottom pair analogously.

We'll analyze chains and cycles separately. It turns out that each chain can be solved with at most one additional empty parking spot. Similarly, each cycle requires at least one empty parking spot and each cycle can be solved with at most two empty parking spots.

Observation 1: A chain with no top pair can be solved with no additional empty parking spots. Note that every chain must contain at least one bottom pair. In this case there is exactly one. The image below depicts how to solve such a chain.

Observation 2: A chain with a top pair requires at least one additional empty parking spot. Furthermore, one parking spot is sufficient. Starting from one end of the chain, we can find the first time a top pair appears and move this top pair to the empty parking spot. We are now left with two chains, where one of them requires no additional parking spots. We first solve this chain, giving us an additional empty parking spot, and then continue solving the other chain. The image below depicts this process.

Observation 3: A cycle with at most one top pair can be solved with only one additional empty parking spot. If there are no top pairs, then the top vehicles of the cycle are a permutation of the bottom ones. We can solve this case by removing any top vehicle to an empty parking spot, reducing the problem to a chain as in observation 1. If the cycle contains exactly one top pair, it contains exactly one bottom pair as well. We move the top pair to an empty parking spot, reducing the problem to a chain as in observation 1.

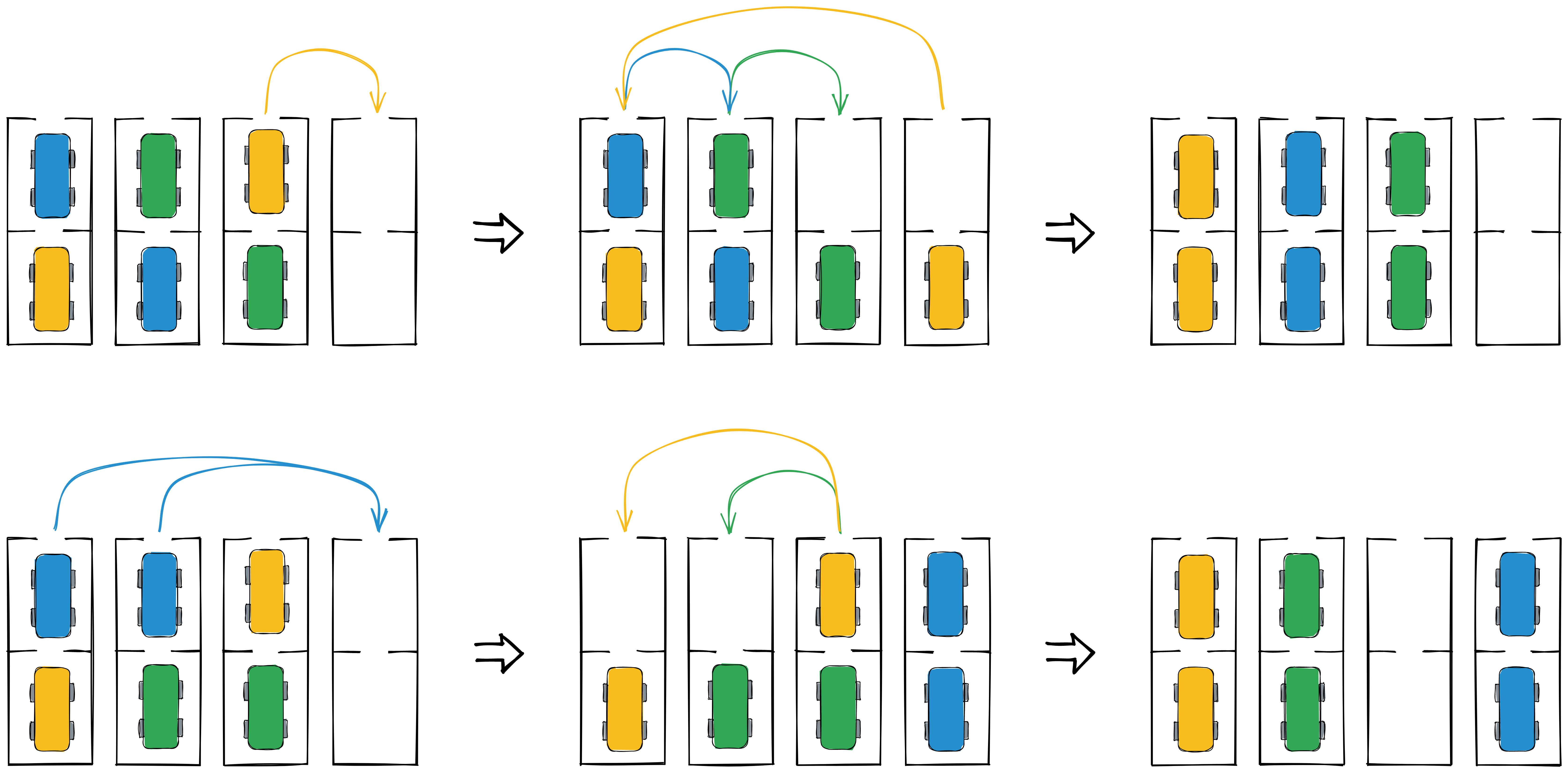
Observation 4: A cycle with more than one top pair requires at least two empty parking spots. We can take any top pair, and move it to an empty parking spot, reducing the problem to a chain as in observation 2.

Combining these observations yields a full solution. Note that we should prioritize solving chains, over solving cycles, because after solving a chain we gain an additional empty parking spot. Similarly, we should prioritize chains and cycles with a smaller number of top pairs.

The subtasks were intended to be solved by using only a subset of these observations, or by alternative approaches. Everything mentioned above can be implemented in ~\mathcal O(N)~ or ~\mathcal O(N \log N)~. The subtasks where ~N \le 1000~ allow for slower solutions with easier implementation.

Subtask 2 can be solved by first moving all top pairs to empty parking spots. There will always be enough space because ~2N \le M~. After that, we are left with only chains and cycles that can be solved as described in observations 1 and 3.

Subtasks 3 and 4 contain no chains. The following greedy approach works for this case:

• if at some point we can pair a vehicle with another one of the same color, we do it,
• otherwise, if there is a top pair, move it to an empty parking spot,
• otherwise, move any vehicle from the top to an empty parking spot.

If at any point there are no parking spots available, there is no solution. Note that this approach does not work for the other subtasks because we should prioritize moving top pairs from chains.