Let's formally define the condition from the task that says that no car can wait with none of the workers. Let's denote some car ~i~ and some worker ~j~. By the time worker ~j~ is done with car ~i+1~, worker ~j+1~ must be done with car ~i~. Note that worker ~j+1~ can finish car ~i~ before this. If car ~i+1~ is sent ~t_0~ minutes after car ~i~, the following must hold:

$$\displaystyle t_0 + \sum_{k=0}^j F_{i+1} T_j \ge \sum_{k=0}^{j+1} F_i T_{j+1}$$

In other words, the time that it takes car ~i+1~ to pass through all the workers up to and including ~j~ must be at least the time that takes car ~i~ to go through workers up to and including ~j+1~.

If we denote by ~S_j~ sum of ~T~ for workers through ~j~, than minimum ~t_0~ for cars ~i~ and ~i+1~ can be written as:

$$\displaystyle t_0 = \max\{F_i S_{j+1} - F_{i+1} S_j \mid 0 \le j \le N-2\}$$

From this, we can derive the brute-force solution. For each ~i~, we go through all the workers to find the maximum value ~t_0~, and we sum up these maximum values with ~F_{M-1} S_{N-1}~. This solution has a complexity of ~\mathcal O(NM)~.

We can come up with a faster solution by taking a look at the expression that we must maximize. Since ~i~ is fixed and all the factors are positive we can divide this expression by ~F_{i+1}~. If we denote this quotient ~F_i/F_{i+1}~ with ~x~, we get ~f(x) = S_{j+1} x - S_j~, i.e. a line equation. For each ~j~ that satisfies mentioned limits, we get a line in the plane. From these lines, we must find the one that gives the maximum value for some ~x~.

This idea is often useful in algorithmic competitions, so we will describe it here in the general case. Let's take a look at how this maximum of lines looks like.

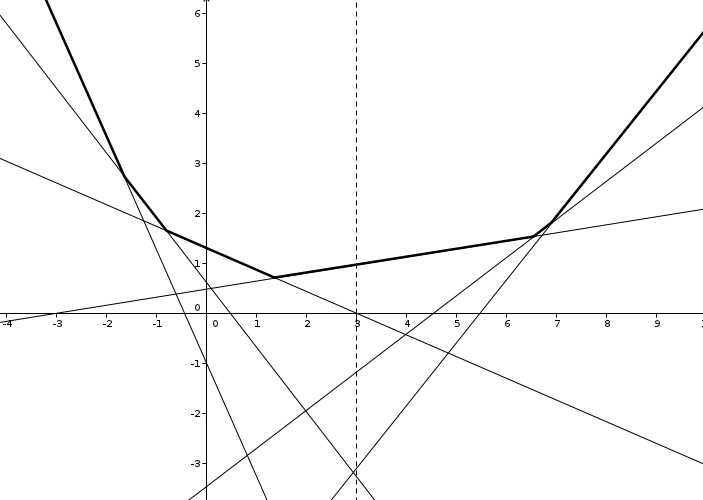
It's a polygonal line enclosing a convex region of the plane. Lines that are part of this line are sorted in increasing order of their slopes. Also, no line is above the previous two lines. This leads us to the following algorithm.

We sort the lines in increasing order of slopes. We push the first two to the stack, and proceed to traverse the rest of the lines. When processing the next line in order, we pop the top line of the stack, as long as the intersection of the top two lines on the stack is below the current line. When this is no longer true, we push the current line to the stack.

We denote the ~i^\text{th}~ line that's pushed on the stack by ~f_i(x)~.

We can find the maximum value for some ~x~ by using binary search, since ~f_i(x)~ is monotonic with respect to ~i~.

The complexity of this approach is ~\mathcal O((N+M) \log N)~, or to be more precise, ~\mathcal O(N \log N + M \log H)~ where ~H~ is the number of lines that are part of the convex boundary.

There is also an alternative solution that represents the expression we are trying to maximize using dot product, and uses convex hulls.