Mister No (real name Jerry Drake) is a comic book character who frequently gets himself into a lot of trouble, which he is usually able to get out of. However, this time it's not so easy. He was searching for ancient Mayan treasures and, in the process, stumbled upon a lost temple. Inside the temple there is a large hall, and inside the hall stands a stone Totem with inscriptions that are the key to understanding the purpose of life $(42)$. However, getting to the Totem is a great challenge.

The Totem is situated on the opposite side of the hall form the entrance. The floor of the hall is covered with stone tiles that bear a striking resemblance to domino tiles. Each tile is divided into two halves (squares), and each half has a number from one to six, inclusive, chiseled into it. Tiles are arranged in $N$ rows, with $N$ tiles in each odd-numbered row and $N-1$ tiles in each even-numbered row. The image below corresponds to the first test example $(N=5)$:

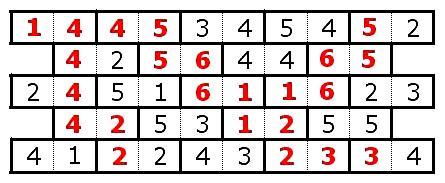
It is only possible to step from one tile to an adjacent one if the two tiles have matching numbers on halves that share an edge. Help Mister No find the shortest path to the Totem by determining the sequence of tiles (outputting the sequence of tiles' labels, described below) that need to be stepped on, in order, from the first to the last tile on the path. If there is no possible path to the Totem, find the shortest path to the tile with the largest label (so that Mister No can make a heroic jump). The stone tiles are labelled in row-major order: in the first row, the first tile has the label $1$, and the last one $N$; in the second row, the first tile is $N+1$, and the last one $2\cdot N-1$, and so on. The entrance leads to the tile with label $1$, and the totem is on the last tile in the last row. Mister No always starts from the entrance.

Input Specification

The first line of input contains the positive integer $N$ $(1\le N\le 500)$, the number of stone tile rows.

Each of the following $N\times N-\frac{N}{2}$ lines (where / stands for integer division) contains two positive integers $A_i$ and $B_i$ $(1\le A_i,B_i\le 6,1\le i\le N\times N-\frac{N}{2})$, the values chiseled into the left and right halves, respectively, of tile $i$.

Output Specification

The first line of output must contain the length (in tiles) of the required shortest path.

The second line of output must contain a sequence of space-separated positive integers, the labels of tiles on the shortest path. As there can exist more than one shortest path, output any one of them.

Scoring

If only the first line of output is correct, the solution is awarded $50\mathrm{\%}$ of points for that test case.

Sample Input 1

5
1 4
4 5
3 4
5 4
5 2
4 2
5 6
4 4
6 5
2 4
5 1
6 1
1 6
2 3
4 2
5 3
1 2
5 5
4 1
2 2
4 3
2 3
3 4

Sample Output 1

7
1 2 7 12 17 22 23

Sample Input 2

3
1 2
2 3
6 6
2 4
3 5
6 6
4 5
5 6

Sample Output 2

4
1 2 5 8

Sample Input 3

4
1 5
5 3
5 5
5 6
5 3
6 4
4 5
2 5
2 4
4 3
2 4
5 2
1 4
1 6

Sample Output 3

7
1 5 8 12 9 10 13