COCI '17 Contest 5 #2 Spirale
View as PDFLittle Stjepan often likes to go out with his friends and have fun in a popular nightclub in Zagreb. However, Stjepan sometimes drinks too much soda and gets light headed from all the sugar. Last night was an example of this, which is why Stjepan had the same image in his mind the whole time. It was a scribble of number spirals of some sort. Since he can't quite remember what the image looked like, but can describe it, he is asking you to reconstruct it for him.
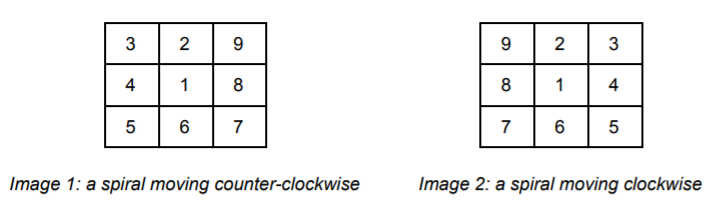
Stjepan recalls that the image was of the shape of a table consisting of numbers written in
- Initially, the table is empty, and each spiral is in its own starting position.
- In each following step, each spiral moves to its next position. It is possible that, at times, the spirals leave the boundaries of the table, but also to return within it.
- After exactly
Input Specification
The first line of input contains positive integers
Each of the following
Output Specification
You must output
Scoring
In test cases worth
Sample Input 1
3 3 1
2 2 0Sample Output 1
9 2 3
8 1 4
7 6 5Sample Input 2
3 3 1
2 2 1Sample Output 2
3 2 9
4 1 8
5 6 7Sample Input 3
3 3 2
1 1 0
1 2 0Sample Output 3
1 1 4
6 5 5
19 18 17Explanation for Sample Output 3
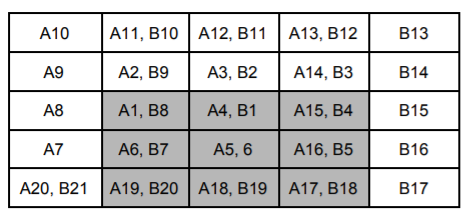
For simplicity's sake, the letter
Comments
T is not necessarily a positive integer (could be 0).