Editorial for COCI '19 Contest 4 #3 Holding
Submitting an official solution before solving the problem yourself is a bannable offence.
The solution of the first subtask is based on dynamic programming where the state is a bitmask. We leave the rest of the details as a practice to the reader.
In the second subtask, it is known that , which means that we can swap numbers on positions
only with numbers on positions from
to
(the rest of the solution assumes that the word interval refers to the agreed interval
). The first important observation is that we will never change the position of a certain number more than once. The second important observation, and much less obvious than the first, is that we only care about which elements were chosen to be swapped within the interval and which were chosen to be swapped outside the interval. Regardless of the way in which we have swapped these numbers, their total cost will remain invariant. For example, if we decided to swap positions
and
from within the interval with positions
and
that are outside the interval, it doesn't matter whether we have changed
with
and
with
or
with
and
with
. We leave the formal proof of this claim as an exercise to the reader.
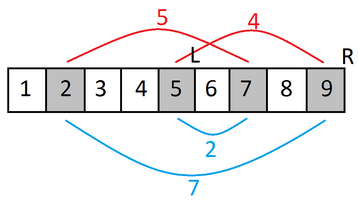
Now it is obvious that the only important thing left is to decide which elements should be chosen from inside and which elements should be chosen from outside of the interval and that the number of chosen elements from inside equals the number of chosen elements outside of the interval. We can achieve that using whose arguments are the current position outside the interval, current position inside the interval and the total amount of money we have spent thus far. The
function returns the maximum decrease in the sum of elements in our interval. The initial state of
is
and the state where we will find our solution is
.
The first transition tells us not to take an element on position
, the second transition tells us not to take an element on position
, while the third transition tells us to take both elements and swap them, thus spending
kunas.
The complexity of this algorithm is .
This algorithm is therefore fast enough for the whole solution, but doesn't include the swaps from the right side of the interval because . Suppose that the optimal solution takes
elements left of the interval,
elements right of the interval and
elements from inside the interval. It is obvious that, if we sort positions of elements we took from within the interval, first
elements will be swapped with the
chosen elements on the left side and next
elements will be swapped with the
chosen elements on the right side. This leads us to a conclusion that there is a line between positions within the interval which determines that all elements from the interval left of that line will be swapped with chosen elements left of the interval, and vice versa for the right side. Since we don't know where that line might lie and since we don't actually care how many swaps are made on each side of an interval, we can place that line on each position within the interval. We can do that with the following lines of code:
for i in range (L-1, R+1):
for j in range (0, K+1):
sol = max(sol, dpL(L-1, i, j) + dpR(R+1, i+1, K-j))What are dpL and dpR? dpL is the same from the last subtask and
dpR is completely identical to it but is being done from the other side. The complexity of each is
and the complexity of merging their solutions is
. Therefore, the total complexity of the algorithm is
.
Why can't you score all the points with that solution then? Because a tridimensional array of the form int dp[N][N][K] takes up too much memory for , but it fits for
. Therefore, we still need to optimize our memory consumption. There are multiple ways to achieve that, but perhaps the easiest is to note that, in the worst case for any
,
and
, the maximum amount of money Ivica needs to perform all swaps is going to be bounded by
. Luckily, arrays of the form
int dp[N][N][N*N/4] fit into the given memory limit of 256 MiB. There is another optimization which swaps the dimension with a smaller constant.
Comments