Afrika paprika! – S.V.

After a tiring morning in the garden, Mr. Malnar decided to reward himself with dried hot peppers he grew himself.

He has ~n~ peppers, connected with ~n-1~ pieces of string, so that every two peppers are connected by some series of strings. Formally, they form a tree.

Mr. Malnar will partake in three lunches today. For that purpose, he will cut two strings to get three smaller components, one for each lunch.

The tree from the third example along with the optimal cuts.

It's bad to make any lunch too spicy, so he will choose the cuts in a way that minimizes the difference between the size of the largest and the smallest component. You need to determine the sought minimum difference.

Input

The first line contains an integer ~n~, the number of peppers. The peppers are labeled by integers from ~1~ to ~n~.

Each of the following ~n-1~ lines contains two integers ~x~ and ~y~ ~(1 \le x, y \le n)~ – labels of peppers that are directly connected by a piece of string.

Output

Print the minimum possible difference of component sizes.

Scoring

Subtask	Score	Constraints
~1~	~15~	~3 \le n \le 200~
~2~	~35~	~3 \le n \le 2\,000~
~3~	~60~	~3 \le n \le 200\,000~

Sample Input 1

4
1 2
2 3
3 4

Sample Output 1

1

Explanation for Sample Output 1

In the first example, each of the possible three ways of cutting the strings yields one component with two peppers and two components with one pepper each. Therefore the answer is ~2-1 = 1~.

Sample Input 2

6
1 2
1 3
3 4
3 5
5 6

Sample Output 2

0

Explanation for Sample Output 2

In the second example, it's possible to get three components of the same size by cutting the string that connects peppers ~1~ and ~3~, and also ~3~ and ~5~, so the answer is ~0~.

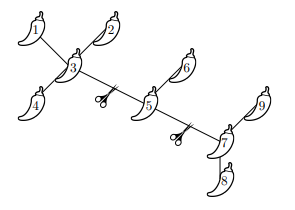
Sample Input 3

9
1 3
2 3
3 4
3 5
5 6
5 7
7 8
7 9

Sample Output 3

2

Explanation for Sample Output 3

Optimal cuts for the third example are shown on the figure in the statement. The sizes of the components are ~4~, ~2~ and ~3~, and the answer is ~4-2 = 2~.