Sadly, this is the last time Sean will play James Bond.

His mission is to network ~n~ antennas that are scattered across a vast desert, which can be represented as a 2D plane. He will set the transmission radius of each antenna to be the same non-negative real number ~r~. The range of an antenna is defined as the set of all points whose distance to the antenna is at most ~r~. If ranges of two antennas have a common point, those antennas can directly communicate. Also, if antennas ~A~ and ~B~ can communicate, as well as antennas ~B~ and ~C~, then antennas ~A~ and ~C~ are also able to communicate, through antenna ~B~.

Sean wants to network the antennas, i.e. make it possible for every two antennas to communicate. Since M has limited his spending for this mission, and larger radii require more money, Sean will choose the smallest possible radius ~r~. Help him solve this problem!

Input

The first line contains an integer ~n~ ~(1 \le n \le 1\,000)~, the number of antennas.

Each of the following ~n~ lines contains integers ~x_i~ and ~y_i~ ~(0 \le x_i, y_i \le 10^9)~, coordinates of the ~i~-th antenna.

Output

Output the minimal radius.

Your answer will be considered correct if its absolute or relative error doesn't exceed ~10^{-6}~.

Scoring

In test cases worth ~50\%~ points it holds that ~1 \le n \le 100~.

Sample Input 1

2
1 1
2 2

Sample Output 1

0.7071068

Sample Input 2

7
2 3
3 4
4 5
0 1
3 1
4 2
1 5

Sample Output 2

1.4142135

Explanation for Sample Output 2

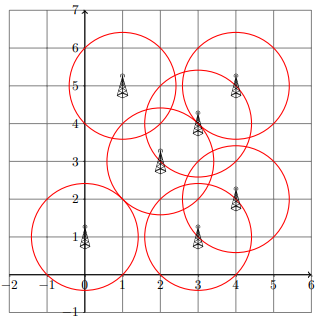
Sample Input 3

4
2020 20
20 2020
2020 2020
20 20

Sample Output 3

1000.0000000