Tin is a very special boy. He doesn't like a lot of things, for example he doesn't like Barcelona, getting defeated in video games or any sort of mess…

Today he is visiting his friend Ante to once and for all decide who is the best FIFA player. The moment he entered Ante's apartment, he was greeted with an unpleasant surprise. Ante has two shelves on his wall side by side. The left one contains $n$ books about the numerous accomplishments of Barcelona stacked on top of each other, and the right one is empty.

He didn't mind so much that Ante was reading, in his opinion, trashy books, but what bothered him much more was that the books were a total mess, that is, they weren't sorted from thinnest to thickest. As Ante is a good friend, he immediately hurried to rearrange the books to Tin's liking. In one move he can:

• take a book from the top of some shelf in his left or right hand, if he is not holding some other book in that hand; or

• put the book he is holding in some hand on top of some shelf.

Ante's strong suit is football, not rearranging books, so he asks you to find some sequence of moves, that he will then perform, so that in the end all books will be on the left shelf and sorted from thinnest to thickest, in the order from top to bottom.

Input

The first line contains an integer $n$ $(1\le n\le 100)$, the number of books on the left shelf.

The second line contains $n$ integers $d_i$ $(1\le d_i\le 1000)$ that represent the thicknesses of the books, from top to bottom.

Output

In the first line output an integer $k$ $(0\le k\le 100000)$, the number of moves in your solution.

In the following $k$ lines output the moves in the form INSTRUCTION HAND SHELF, where:

• INSTRUCTION is the word UZMI (Croatian for take) if Ante should take a book from some shelf, or the word STAVI (Croatian for put) if he should put a book on some shelf

• HAND is the letter L if Ante should use his left hand, or the letter D (Croatian word for right is desno) if he should use his right hand

• SHELF is the letter L if this move acts on the left shelf, or the letter D if it acts on the right shelf.

Your solution does not have to be of minimum possible length, but the number of moves must not exceed $100000$. It can be proven that for the given constraints a solution always exists.

Sample Input 1

3
2 3 1

Sample Output 1

8
UZMI L L
STAVI L D
UZMI L L
UZMI D L
STAVI L L
UZMI L D
STAVI L L
STAVI D L

Explanation for Sample Output 1

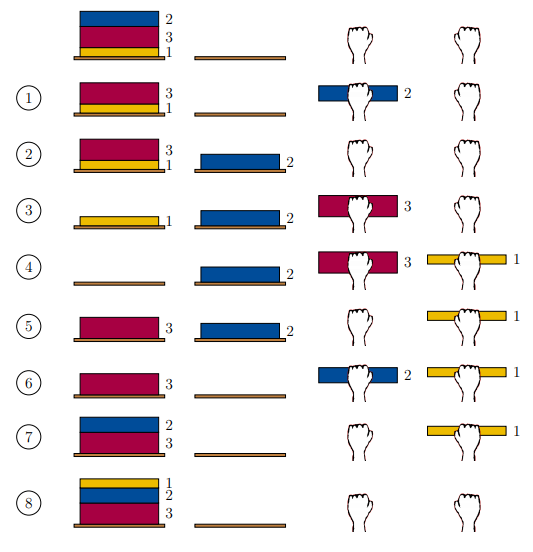
Sample Input 2

4
1 1 2 5

Sample Output 2

0