COCI '20 Contest 4 #4 Janjetina
View as PDFAfter restaurants all over Croatia closed because of the lockdown, Mr. Malnar was first overwhelmed with sadness. But he soon realized that there was no point in being sad, and he decided that as soon as the restaurants reopen, he will travel around Croatia and treat himself with the best lamb Croatian restaurants can offer.
Mr. Malnar knows about cities he could visit, that he labeled with integers from
through
. Also, he knows about
two-way roads that connect those cities, in such a way that it is
possible to travel between any two cities.
On every road there is a restaurant that serves lamb, and Mr. Malnar knows how many kilograms of lamb he can order in each one.
He will choose two different cities and
, and travel from
to
via the shortest path, i.e. the path
that uses the minimal number of roads. He will stop at exactly one restaurant, the one where he can
order the maximum amount of lamb (if there are multiple such restaurants, he will choose any of them),
and he will of course eat all the lamb he orders.
Mr. Malnar considers a path of length on which he eats
kilograms of lamb to be satisfactory if
. The length of a path is equal to the number of roads that it goes through.
He wonders how many ordered pairs of distinct cities there are, such that the shortest path from
to
is satisfactory. He is very busy, so he asks you to calculate the answer for him.
Input Specification
The first line contains integers and
, the number of cities, and the satisfaction threshold.
Each of the following lines contains three integers
,
and
, which means that there is a road that connects
and
, and there is a restaurant on that road where Mr. Malnar can order
kilograms of lamb.
Output Specification
Output the number of ordered pairs of distinct cities , such that the shortest path from
to
is satisfactory.
Constraints
| Subtask | Points | Constraints |
|---|---|---|
| Cities |
||
| No additional constraints. |
Sample Input 1
3 2
1 2 3
1 3 2Sample Output 1
2Sample Input 2
4 1
1 2 1
2 3 2
3 4 3Sample Output 2
6Sample Input 3
5 2
1 2 2
1 3 3
3 4 2
3 5 4Sample Output 3
8Explanation for Sample 3
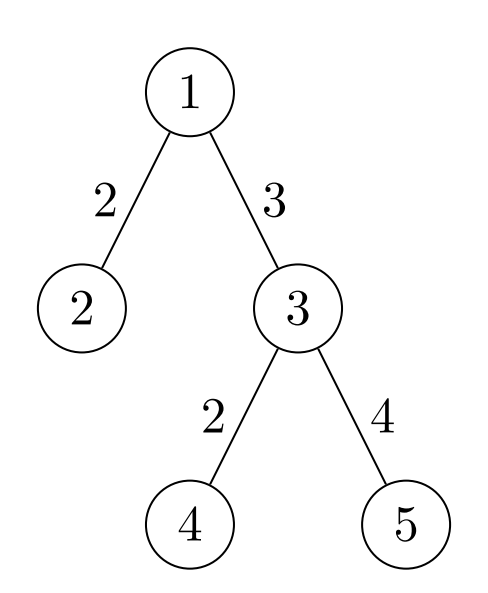
The pairs are ,
,
,
,
,
,
and
.
Comments