Paula and Marin are playing a game on a tree. Not on a real tree, of course. That would be dangerous. Although, who can say that a connected graph with $n$ nodes, marked by integers from $1$ to $n$, and $n-1$ edges, is completely safe?

Before the game started, Paula colored some edges blue, and Marin colored some edges red. If some edge was colored by both, its final color is magenta. All edges were colored by at least one of them.

Paula's piece starts the game in node $a$, and Marin's piece in node $b$. Players alternate moves, and Paula goes first. When it's their turn, the player must move their piece to some adjacent node which doesn't also contain the opponent's piece. Also, Paula can't use red edges, and Marin can't use blue edges, while both can use magenta edges. The player who can't make a move loses.

Paula and Marin both play optimally. If they realize that the game can run forever, they will declare a draw. Determine the outcome of the game!

Input Specification

The first line contains an integer $n$ $(2\le n\le 100000)$, the number of nodes.

The second line contains integers $a$ and $b$ $(1\le a,b\le n,a\ne b)$, initial nodes of Paula and Marin.

The next $n-1$ lines describe the edges. Each line is of the form x y color, where x and y $(1\le x,y\le n)$ are the endpoints, and color is plava (Croatian for blue), crvena (Croatian for red) or magenta.

Output Specification

Output Paula if Paula will win, Marin if Marin will win, or Magenta if it's a draw.

Constraints

Subtask	Points	Constraints
1	30	$2\le n\le 100$
2	30	All colors are magenta.
3	50	No additional constraints.

Sample Input 1

3
1 3
3 2 magenta
2 1 magenta

Sample Output 1

Paula

Explanation for Sample Output 1

Paula will move to node $2$, and then Marin can't make a move.

Sample Input 2

5
3 5
1 2 magenta
1 3 magenta
2 4 plava
2 5 crvena

Sample Output 2

Marin

Explanation for Sample Output 2

Paula must move to node $1$, and then Marin will move to node $2$. Paula now can't move to node $2$, since Marin is there, so she must return to node $3$. Marin moves to node $1$ and wins.

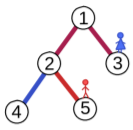
Sample Input 3

5
1 4
2 1 plava
1 3 crvena
5 2 plava
4 1 magenta

Sample Output 3

Magenta