Editorial for COCI '20 Contest 6 #4 Geometrija

Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.

The first subtask can be solved in $\mathcal O(n^4)$ ~\mathcal O(n^4)~ complexity by simply checking for each segment if it crosses with other segments.

To check if two segments cross, we will use the function

$\displaystyle ccw(A, B, C) = x_A \cdot (y_B-y_C) + x_B \cdot (y_C-y_A) + x_C \cdot (y_A-y_B)$

This is equal to twice the signed area of the triangle $ABC$ ~ABC~ (which is not important in this task), and is positive when $A$ ~A~, $B$ ~B~ and $C$ ~C~ are in counterclockwise order (ccw order for short).

Segments $\overline{AB}$ ~\overline{AB}~ and $\overline{CD}$ ~\overline{CD}~ cross if and only if

$\displaystyle ccw(A, B, C) \cdot ccw(A, B, D) < 0\text{ and }ccw(C, D, A) \cdot ccw(C, D, B) < 0$

(since the points are in general position in this task, we don't have to deal with special cases that would arise if some three were collinear). The proof is left as an exercise to the reader.

We say a segment is good if it doesn't cross with any other segment. For the rest of the solution, we use the observation that every good segment necessarily belongs to every triangulation of the given set of points. Triangulation of some set of points on the plane is a division of the convex hull into triangles with vertices in given points, such that every point is a vertex of at least one triangle. Equivalently, it is a maximal set of non-crossing segments between the given points. A triangulation can have at most $3n-6$ ~3n-6~ segments, so if we find some triangulation, we get just $\mathcal O(n)$ ~\mathcal O(n)~ candidates for good segments. The proof of the claims above is left as an exercise to the reader.

Therefore, the second subtask can be solved in $\mathcal O(n^3)$ ~\mathcal O(n^3)~ complexity. We can build a triangulation in $\mathcal O(n^3)$ ~\mathcal O(n^3)~ by going through all the segments, checking if it crosses with the already added segments, and if not, we add it to the triangulation. We then check for every segment we added, in $\mathcal O(n^2)$ ~\mathcal O(n^2)~ complexity, if it crosses with each possible segment.

We will solve the third subtask in complexity $\mathcal O(n^2 \log n)$ ~\mathcal O(n^2 \log n)~. Finding a triangulation is the easy part. There is a lot of ways to do it, fastest in complexity $\mathcal O(n \log n)$ ~\mathcal O(n \log n)~, but we will describe an easier algorithm with $\mathcal O(n^2)$ ~\mathcal O(n^2)~ complexity. First, we find the convex hull, and triangulate that polygon in some way (for example by taking all diagonals from some point). Then, we go through all interior points, find the triangle that contains the current point, and divide it into three smaller triangles.

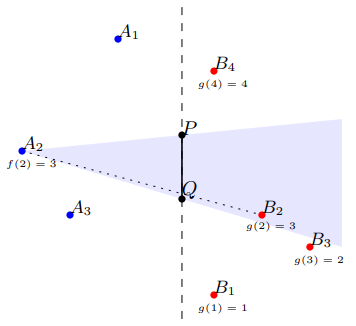
Now we describe how to check in $\mathcal O(n)$ ~\mathcal O(n)~ complexity if some segment is good. Consider a segment $\overline{PQ}$ ~\overline{PQ}~. To make it easier to describe the solution, imagine without loss of generality that the line $PQ$ ~PQ~ is vertical and $P$ ~P~ is above $Q$ ~Q~, as in the figure below. Let $A_1, \dots, A_s, B_1, \dots, B_t$ ~A_1, \dots, A_s, B_1, \dots, B_t~ be all other points, in ccw order around $P$ ~P~, so that for all $A_i$ ~A_i~ it holds $ccw(P, Q, A_i) < 0$ ~ccw(P, Q, A_i) < 0~, and for all $B_j$ ~B_j~ it holds $ccw(P, Q, B_j) > 0$ ~ccw(P, Q, B_j) > 0~ (see the figure).

Consider some point $A_i$ ~A_i~. Let $f(i)$ ~f(i)~ be the maximum $j$ ~j~ such that $ccw(A_i, P, B_j) < 0$ ~ccw(A_i, P, B_j) < 0~ (if it exists). Points $B_1, \dots, B_{f(i)}$ ~B_1, \dots, B_{f(i)}~ are exactly those points on the right side that are below the line $A_i P$ ~A_i P~. It's easy to see that $f$ ~f~ is increasing, so it can be calculated using the two pointers method.

Consider the ccw order of points $B_1, \dots, B_t$ ~B_1, \dots, B_t~ around $Q$ ~Q~ (where we take the first point to be the one with maximum angle $\angle PQB_j$ ~\angle PQB_j~). Let $g(j)$ ~g(j)~ be the position of $B_j$ ~B_j~ in this order.

Let $j' = \arg\max_{1 \le j \le f(i)} g(j)$ ~j' = \arg\max_{1 \le j \le f(i)} g(j)~ (the $j$ ~j~ among $1, \dots, f(i)$ ~1, \dots, f(i)~ for which $g(j)$ ~g(j)~ is maximal). We claim that it's enough to check if segment $\overline{A_i B_{j'}}$ ~\overline{A_i B_{j'}}~ crosses with segment $\overline{PQ}$ ~\overline{PQ}~, i.e. if it doesn't, then the segment $\overline{A_i B_j}$ ~\overline{A_i B_j}~ for any other $j$ ~j~ also doesn't cross with $\overline{PQ}$ ~\overline{PQ}~.

It's clear that $\overline{A_i B_j}$ ~\overline{A_i B_j}~ and $\overline{PQ}$ ~\overline{PQ}~ cross if and only if point $B_j$ ~B_j~ is below the line $A_i P$ ~A_i P~ and above the line $A_i Q$ ~A_i Q~. Among the right points that are below $A_i P$ ~A_i P~, point $B_{j'}$ ~B_{j'}~ is "furthest around $Q$ ~Q~", so if it's below $A_i Q$ ~A_i Q~, then all other points are too.

So, for each point $A_i$ ~A_i~ we need to find its $j'$ ~j'~ (it can easily be updated when we calculate $f$ ~f~) and check whether segments $\overline{A_i B_{j'}}$ ~\overline{A_i B_{j'}}~ and $\overline{PQ}$ ~\overline{PQ}~ cross. If there is no such $i$ ~i~, then $\overline{PQ}$ ~\overline{PQ}~ is a good segment.

The ccw order of points around some center point can be found directly by sorting the points in $\mathcal O(n \log n)$ ~\mathcal O(n \log n)~ complexity. It's worth noting that there exists a (much more complicated) algorithm with $\mathcal O(n^2)$ ~\mathcal O(n^2)~ complexity that determines this for all points together (so the total complexity of the solution of this task would be $\mathcal O(n^2)$ ~\mathcal O(n^2)~). It uses duality to transform it into the line arrangement problem.

Comments

There are no comments at the moment.