Mirko and Slavko stumbled upon an old pinball machine. The game consists of a small metal ball that moves inside the machine, hitting and bouncing off some obstacles.

The game takes place on a board which is represented by a plane and ~n~ obstacles are given in this plane. An obstacle is represented by a line segment of unit length tilted at a ~45^{\circ}~ angle with respect to the coordinate axes. An obstacle is uniquely described by the position of its midpoint ~(x_i, y_i)~ and a character which is either / or \, denoting the orientation of the obstacle. In the plane there is also a ball which is moving in one of the four directions parallel to the axes at all times. If the ball hits an obstacle, the direction of its movement changes by ~90^{\circ}~ and the ball continues moving. Note that the obstacles are two-sided, meaning that the ball is able to bounce off both sides of the obstacle.

Mirko and Slavko decided to restore the pinball machine with a new layer of paint. At their disposal are four buckets of paint containing four different colors. They want to paint each obstacle in one of these four colors.

Mirko: "You know, I've been thinking. There are only two possibilities for the path the ball could take."

Slavko: "What do you mean?"

Mirko: "Well, either the ball will get stuck in a cycle, periodically repeating the same sequence of bounces, or at some point it will fly off to infinity."

Slavko: "Hm, you're right. Then maybe we could try to color the obstacles so that for each cycle each of the colors appears an equal number of times in the cycle and so that this number is even. For example, if some cycle consists of ~24~ bounces, we should make it so that there are ~6~ bounces for each color, and ~6~ is an even number."

Mirko: "And what if there is no such coloring?"

Slavko: "You know the drill, just say -1."

Help Mirko and Slavko determine a coloring of the obstacles which satisfies the required condition, if there is one.

Input Specification

The first line contains a positive integer ~n~ ~(1 \le n \le 500\,000)~, the number of obstacles.

The ~i^\text{th}~ of the next ~n~ lines contains integers ~x_i~ and ~y_i~ ~(0 \le |x_i|, |y_i| \le 10^9)~ and a character ~c_i~ (/ or \) which describe the ~i^\text{th}~ obstacle. No two obstacles have the same position.

Output Specification

If there is no coloring which satisfies the required condition, on one line print -1.

Otherwise, on one line print a sequence of ~n~ numbers 1, 2, 3, or 4 separated by spaces, representing a valid coloring, the colors of the obstacles in order. If there is more than one solution, print any.

Constraints

Subtask	Points	Constraints
~1~	~20~	~1 \le n \le 40~
~2~	~20~	There is at most one cycle in which the ball can get stuck.
~3~	~70~	No additional constraints.

Sample Input 1

4
1 1 \
3 1 /
3 2 \
1 2 /

Sample Output 1

-1

Explanation for Sample Output 1

The ball can be stuck in a cycle of ~4~ bounces, bouncing between the ~4~ given obstacles. To appear an equal number of times, each color should appear once, but one is not an even number.

Sample Input 2

9
1 2 \
1 3 /
2 1 \
2 2 \
2 3 \
3 1 /
3 2 \
4 2 /
4 3 \

Sample Output 2

1 3 2 4 1 3 2 4 1

Explanation for Sample Output 2

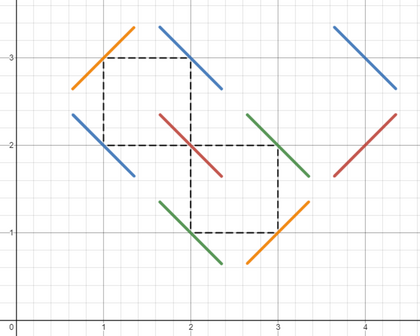
There is only one cycle in which the ball can get stuck. The image below shows a valid coloring. Starting from obstacle ~1~, moving in the clockwise direction the colors repeat 1 3 1 4 2 3 2 4.

Sample Input 3

12
1 2 \
1 3 /
2 1 \
2 2 \
2 3 \
2 4 /
3 1 /
3 2 \
3 3 \
3 4 \
4 2 /
4 3 \

Sample Output 3

1 3 2 4 2 4 1 3 1 3 2 4