Editorial for COCI '22 Contest 1 #2 Čokolade
Submitting an official solution before solving the problem yourself is a bannable offence.
First, let us observe that the order of chocolates, does not matter, so we can sort them. Equivalent to the value is to sum the value
of every chocolate separately. If we need one chocolate, it would be optimal to take the most expensive or the cheapest chocolate. The reason why that is the case is described in the condition of the task:
- If the chocolate is cheaper than
kunas, Lana will pay full price and therefore she would like to take the chocolate with the smallest price possible.
- If the chocolate is more expensive than
kunas, the value
for that chocolate will be equal to
. So, the more expensive chocolate is, the better.
With this, we can solve the first partial. If we split the chocolates into two categories ( and
), we can iterate over the number of cheaper chocolates. If Lana takes
chocolates cheaper than
(first
chocolates in the sorted sequence), she will take
expensive (last
chocolates). Time complexity is
.
Let us look at this example: Consider a query with and
.
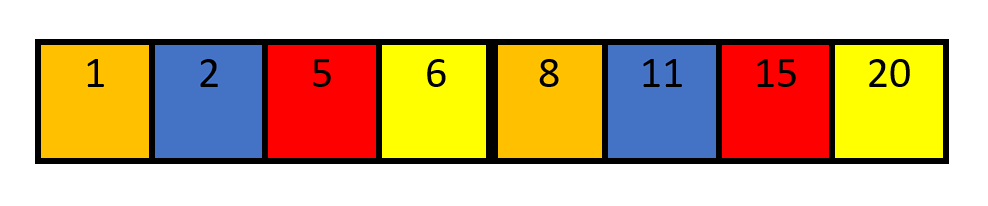
Four numbers are larger than , and four are smaller. Let us assume that we want to take all four chocolates smaller than
. Can we make the required value smaller? The answer is yes. If we would instead of the chocolate that costs
kunas (value
) take the chocolate that costs
kunas (value
), the total value would be smaller. If we compare the next two possible chocolates from the ends (
and
), we can see that
has a value of
, and
has a value of
, so it is even better to take two of the chocolates from the right end! With that step, we have reached the best solution
(because the values of the next two chocolates are
and
, so the chocolate with the price
has a smaller value than the chocolate with the price
). It is enough to binary search the number of chocolates we are taking with the smaller than
for each query with the same check we were making in the paragraph above. For every query that will be
operations. Total time complexity is
.
Comments