COCI '22 Contest 4 #4 Mreža
View as PDF
The city mayor Mirko lives in a city with neighborhoods connected with
bidirectional roads such that from any neighborhood it is possible to reach every
other neighborhood.
Mirko wants to upgrade some roads to reduce traffic. For every road, we know the
current speed vehicles drive on it, the price of upgrading
, and the speed of
driving after upgrading
.
There are unsatisfied citizens that come to visit Mirko. Each one has their
suggestion for an upgrade. The suggestion of the
citizen is: "We should invest
euros in upgrading
roads between neighborhoods
and
."
For each suggestion, Mirko is interested in what is the minimum driving speed between neighborhoods
and
if he spends at most
euros on upgrading the roads, given that his goal is to maximize the
minimum driving speed between the neighborhoods
and
.
Mirko soon realized that calculating this is not an easy task and hired you to help him!
Input Specification
The first line contains the integer
, the number of neighborhoods.
In each of the next lines there are five integers
, denoting that neighborhood
and
are connected,
and the current driving speed is
, the cost of upgrading the road is
, and the speed on the road after upgrading would be
.
The next line contains the integer
, the number of unsatisfied citizens.
In each of the next lines there are three integers
,
which describe the suggestion of the
citizen.
Output Specification
In the of the
lines, print the answer to the request of the
citizen.
Constraints
| Subtask | Points | Constraints |
|---|---|---|
| 1 | 21 | |
| 2 | 29 | Each of the neighborhoods will be connected with at most |
| 3 | 60 | No additional constraints. |
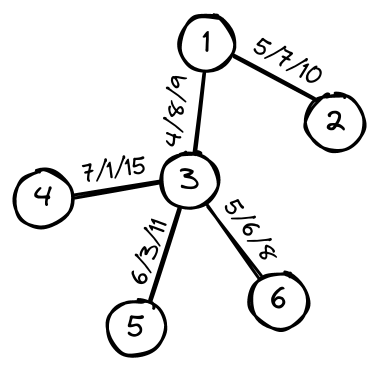
Sample Input 1
6
1 2 5 7 10
1 3 4 8 9
3 4 7 1 15
3 5 6 3 11
3 6 5 6 8
3
2 4 15
6 4 5
3 5 10Sample Output 1
7
5
11Explanation for Sample 1
The illustration represents the city and its neighborhoods. On the edges are written the current driving speed, the cost of upgrading, and the speed after upgrading, respectively.
If we upgrade the roads between and
, and between
and
, the driving speeds from
to
will be
,
, and
m/s. The minimum is
m/s.
If we upgrade the roads between and
, the driving speeds from
to
will be
and
m/s. The
minimum is
m/s.
If we upgrade the road between and
, the driving speed from
to
will be
m/s.
Sample Input 2
4
1 2 5 5 8
2 3 4 6 9
3 4 6 10 7
4
1 4 16
2 4 16
1 4 10
3 4 10Sample Output 2
6
7
5
7
Comments