Prepared by: Patrick Pavić

For solving the first and second subtasks, it was sufficient to attempt a depth-first search on the graph after removing each edge and check if the graph is connected.

To solve the remaining subtasks, similar to the classical algorithm for finding bridges, our algorithm will work with the DFS tree of the given graph. A specific property of the DFS tree is that all edges not in the tree connect a node to one of its descendants. We will refer to nodes of that kind as back edges. The edges that have the property sought in the task will be called good edges.

First, we will check for all edges in the DFS tree to see if they are good edges. This algorithm will not differ much from the algorithm for finding articulation points, and we leave the details to the reader as an exercise. This was sufficient to solve the fourth subtask, while checking the remaining ~m-n+1~ edges using the same algorithm as in the first two subtasks.

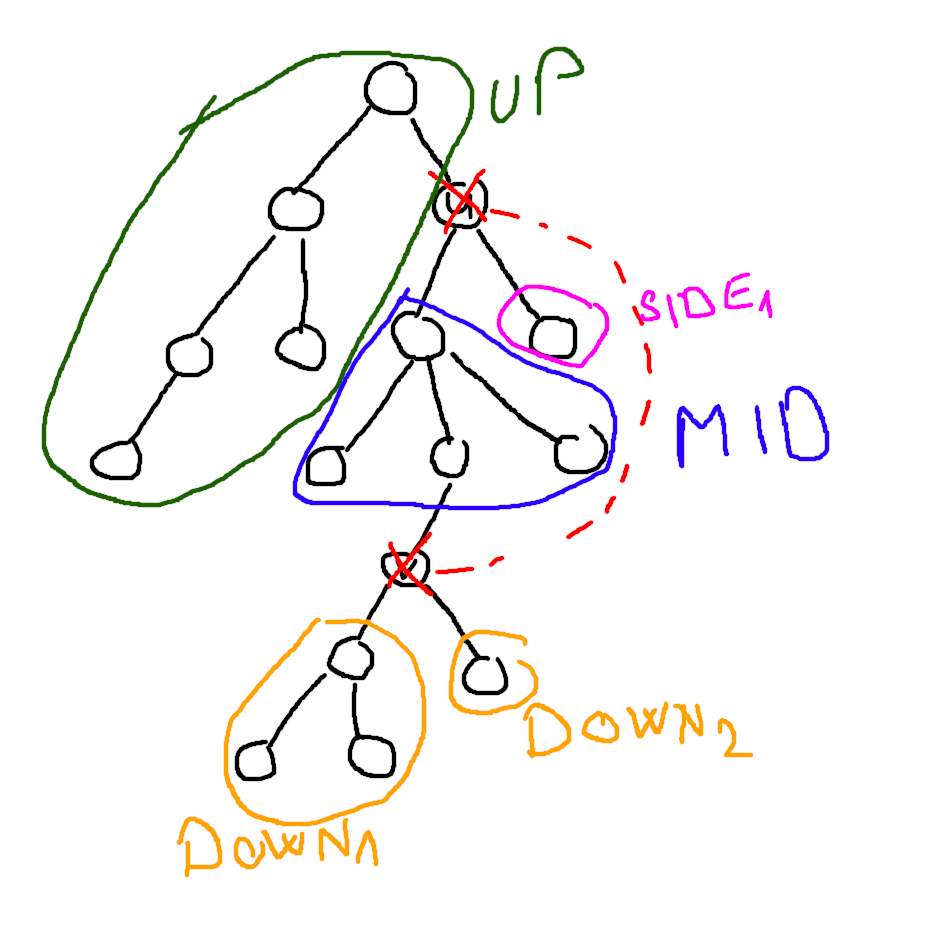
Now, let's consider a back edge ~(u, v)~ and the components formed by its removal. It is necessary to check if these components are connected to each other by back edges. If they are not, that edge is good. These components can be divided into four primary groups:

• ~UP~ - a component that contains the root of the DFS tree (the node from which we initiated the DFS)
• ~SIDE_i~ - the components formed by removing node ~v~ in its subtree, except the one that contains node ~u~
• ~MID~ - a component containing the path between nodes ~u~ and ~v~ (as the edge is not in the tree, this path will always exist)
• ~DOWN_j~ - the components formed by removing node ~u~ in its subtree

Assuming that the graph remains connected, all components of the ~SIDE_i~ group must contain a back edge within them that connects them to the ~UP~ component. Similarly, all components of the ~DOWN_j~ form must have a back edge connecting them either to the ~MID~ component or to the ~UP~ component (note that they cannot be connected to the ~SIDE_i~ component due to the condition of the DFS tree). Finally, to keep the graph connected, at least one of the following two statements must be true:

• There exists a ~DOWN_j~ component that contains both a back edge to the ~UP~ component and to the ~MID~ component.
• There exists a back edge from the ~MID~ component to the ~UP~ component.

All of these conditions can be efficiently checked using various segment trees ordered by the preorder traversal of the DFS tree. One very useful thing is to compute, for each subtree, the highest and lowest back edge leaving that subtree (disregarding back edges completely in the subtree). This was possible to calculate using segment trees or the small to large algorithm. Depending on the implementation, it was achievable to reach a complexity of ~\mathcal O((m+n) \log n)~ or ~\mathcal O((m+n) \log^2 n)~, which was sufficient to solve the problem. Slower implementations solved the third subtask.