Editorial for COI '14 #1 Čvenk
Submitting an official solution before solving the problem yourself is a bannable offence.
In this task, we have to determine the minimum total number of steps necessary in order for all the tourists to meet in the same field of the labyrinth.
According to the image, it seems that the labyrinth is shaped like a tree, and if we set field as the root, field
has a depth of
. This isn't difficult to prove: The case where one of the coordinates is
is trivial (father of
is
, symmetrical for
). Let's denote the lowest active bit of a positive integer
with
. Notice that, because
,
. Let's assume that
(the other case is symmetrical).
We can visualize it this way:
x: ???????????0000...010...000
y: ???????????1000...000...000Let's observe numbers and
:
x-1: ???????????0000...001...111
y-1: ???????????0111...111...111Now it is clear that and
, so the father of field
in the tree is field
, which matches our expectations. If
, the father is
. Therefore, it really is a tree. It needs to be noted that something stronger holds. Specifically, for
,
for
from
, the argument is similar as for
, and this will be useful later for quick calculation of the
ancestor.
The typical next step is to implement the function that finds the lowest common ancestor of fields
and
. First, we will implement an auxiliary function
that finds the
in line ancestor of field
. We can implement it recursively:
kth_ancestor(x, y, k):
if k == 0: return (x, y)
if x == 0: return (x, y - k)
if y == 0: return (x - k, y)
if lobit(x) < lobit(y):
return kth_ancestor(x - min(lobit(x), k), y, k - min(lobit(x), k))
if lobit(x) > lobit(y):
return kth_ancestor(x, y - min(lobit(y), k), k - min(lobit(y), k))
Using this function, we can implement the function using the classical algorithm of jumping on powers of
, in other words, binary search.
From now on, we will denote the fields with letters, instead of coordinates.
Notice that when we have the function we can easily calculate the distance between two nodes
and
in the tree as
.
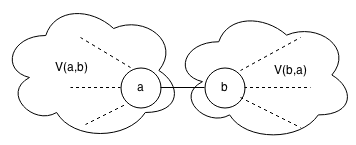
We are left with finding a node where the tourists will meet in. This is a typical tree problem and generally the idea is this: let's assume that we are located in node . Let node
be the neighbour of
, let's observe the edge
. Let
be the number of nodes in the subtree seen from the side of node
(when we are looking at the edge between
and
, image!), and
the same for node
. Then
is a better choice for the meeting if and only if
. Since
, it follows
. It is clear that node
is optimal only if for each of its neighbours
it holds
. The reader is left with making sure that this condition is sufficient too.
Let's get back to the tree from the task (remember, it's rooted). We will denote the number of tourists in the subtree of node in our tree with
. Now we are looking for node
such that
(so that in the part of the tree above
there is no more than
tourists) and
for each child
of
. If we take an initial node, we can easily use binary search and the function
to find the first ancestor
such that
. If all of its children have less than or equal to
tourists in their subtrees, we have found the solution. Checking the number of tourists in a subtree can be done in
by examining for each node with a tourist if it's a descendant of the node we're considering (by calling the function
with the depth difference). Given the fact that in the subtree of the optimal node there are at least
tourists, we can randomly choose one of
nodes with tourists as the initial node for binary search. The expected number of initial nodes we will need to check is
.
After we find the optimal node, we are left with summing up the distances of tourists to our node.
The complexity of function is
, where
is the maximal value of coordinates of a field, so the complexity of finding the optimal node is
,
for binary search and
to check the node (and the expected number of tries is
).
The complexity of function is
,
for binary search,
to call function
. We have to call it
times in order to calculate all distances, so the complexity of this part, as well as the total algorithm complexity, is
.
Comments