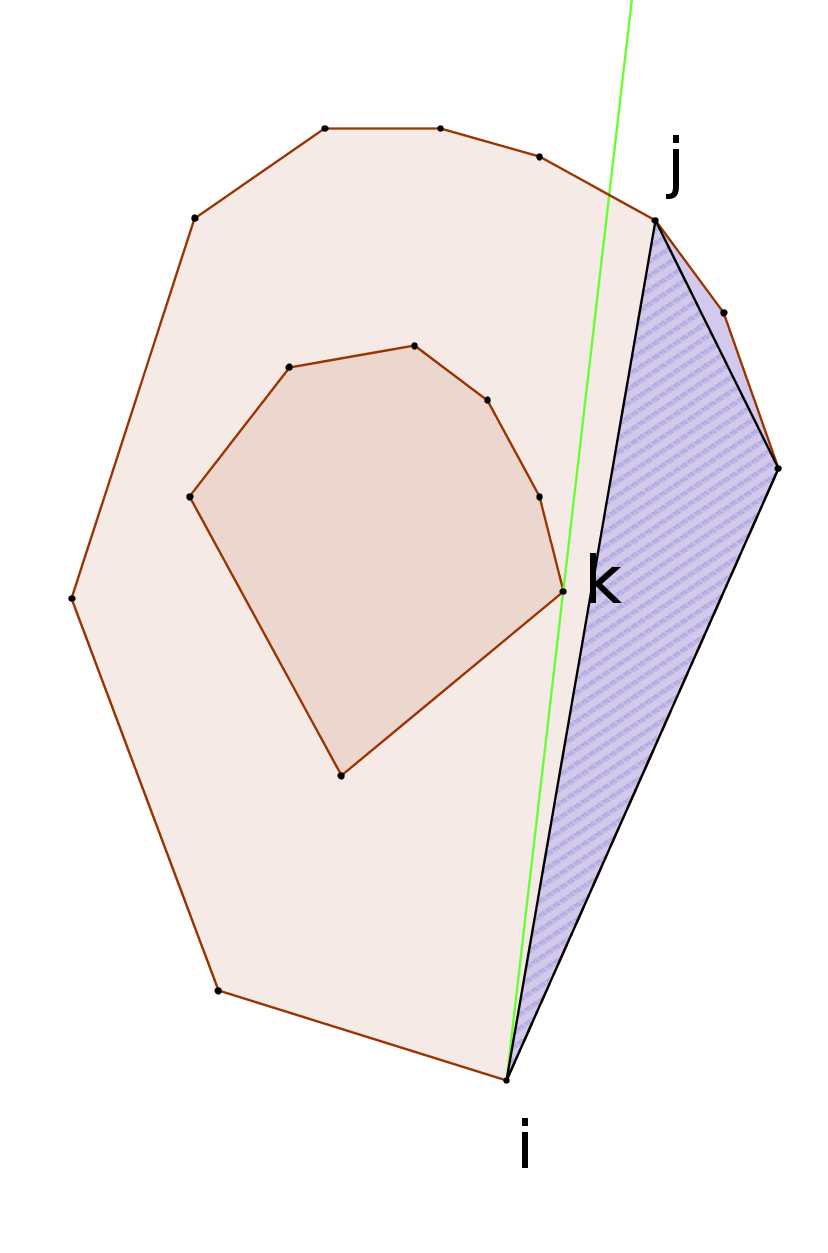
To begin with, let's assume that in the interior of the polygon there are more than two points and not all of them are on the same line. We are only interested in the points on the convex hull from the inner set. For a polygon vertex ~i~ we have the situation as depicted:

The green color marks the tangent in ccw (counter-clockwise) direction to the inner hull, index ~k~ marks the belonging hull vertex, and index ~j~ marks the polygon vertex to which (in ccw direction) we can make the best cut from ~i~. Notice that this will always be the last vertex (starting from ~i~) from the right side of the tangent (looking from ~i~ facing ~k~). The area of the polygon from vertex ~i~ to ~j~ is marked with purple and let's assume it's ~P(i, j)~. If we take the maximum of these areas for each ~i~ (vertex ~j~ is determined with vertex ~i~), we will get the solution.

Let's denote with ~i'~ the vertex adjacent to vertex ~i~ in ccw direction. We are interested in vertex ~k'~ of the inner hull through which the tangent from ~i'~ is going to pass, and vertex ~j'~, the optimal vertex for ~i'~. Let's observe the following image:

Vertex ~k'~ can be found so that we move in ccw direction on the inner hull as long as the next vertex is on the right side of the line from ~i'~ to the current vertex (if we're looking from ~i'~ facing the current vertex). In the image, the vertices for which the next vertex is better are marked with red.

We can find vertex ~j'~ so that we move in ccw direction on the polygon as long as the next vertex is on the right side of the line ~(i', k')~, from ~i'~ facing ~k'~.

Notice that in this procedure we can keep track of the current area. When we move from ~i~ to ~i'~, we subtract the area of the triangle ~(i, i', j)~ (marked in the first image). When we look at index ~j'~, we add the area of the corresponding triangle in each move (those triangles are separated using dotted lines in the second image).

The complexity of finding the convex hull of an inner set of points is ~\mathcal O(M \log M)~. After that, finding the optimal cut is ~\mathcal O(N+H)~, where ~H~ is the number of points on the hull, or ~\mathcal O(N+M)~ in the worst case scenario. Index ~i~ will go through all the points of the outer polygon. Finding the indices ~j~ and ~k~ can be complex in one transition, but in total it's amortised because both indices can visit a point at most once (~j~ on the polygon, ~k~ on the inner hull).