COI '19 #3 Semafor
View as PDFYou are most likely familiar with a so-called -segment display which is widely used to depict digits on
various digital devices, such as watches or calculators. Due to its simplicity, intuitiveness and aestheticism,
this design has been accepted across the globe. Still, young Matej argues against the
-segment design
and claims that the same functionality can be obtained more efficiently, using only
segments.
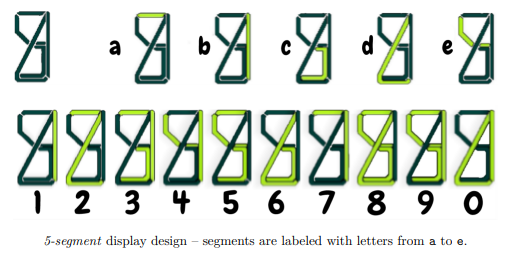
-segment display design – segments are labeled with letters from
a to e.
Matej decided to make his first entrepreneurial steps in the most prosperous branch of Croatian economy, football. His revolutionary design will be used on a substitution board during the games of 1. HNL (the elite tier of Croatian professional football). He is currently making a presentation for the board of directors at the Croatian Football Association.
The substitution board consists of
-segment displays which, from left to right, represent the digits
of a jersey number worn by the player that is about to leave the pitch. At the beginning of Matej's
presentation, the substitution board represents the number
, and Matej will make one of the following
moves each second:
- Turn on one segment that is currently turned off.
- Turn off one segment that is currently turned on.
In total, Matej will make moves and he will make sure that after each
-th move, the board shows a
valid number. The number is valid if each of its digits is correctly shown on the corresponding display
(i.e. segments that are turned on show a valid digit). Also, numbers having less than
digits are validly
shown if they contain the appropriate number of leading zeros.
For each final state (integer between and
), Matej is interested in how many different ways could
he make his moves during the presentation such that this final state is reached at the end. Of course, he
needs to adhere to all limitations presented in the previous chapters. We consider two sequences of moves
different if, imagining they are executed on two different boards at the same time, there is a moment at
which the two boards represent a different state.
Since the number of different ways can be quite large, you are asked to compute it modulo .
Input Specification
The first line contains integers
, and
from the task description.
Output Specification
In the -th line, you should output the number of different ways for the substitution board to show the
number
at the end of Matej's presentations. The numbers should be printed modulo
.
Constraints
| Subtask | Points | Constraints |
|---|---|---|
| 1 | 6 | |
| 2 | 15 | |
| 3 | 12 | |
| 4 | 12 | |
| 5 | 15 | |
| 6 | 40 |
Sample Input 1
1 2 1 5Sample Output 1
0
0
0
1
0
2
0
0
0
0Explanation for Sample Output 1
At the beginning of the presentation, the (single-digit) substitution
board shows the number . After each move (due to
), the board must show a valid number. Matej
is going to make a total of
moves. Therefore, at the end of the presentation, the board can show
either number
or number
. Number
can be obtained using one way (
) and number
can be
obtained using two ways (
and
).
Sample Input 2
1 3 3 8Sample Output 2
0
0
0
6
0
13
0
0
0
0Sample Input 3
1 4 2 4Sample Output 3
24
0
8
0
37
0
4
28
4
24
Comments