DMOPC '14 Exam Time P4 - Exam Delay
View as PDFYou wake up on the day of the exam and realize that these questions were useless!
Fortunately, a certain Math Teacher "volunteered" to proofread the original copies of all the exams to ensure their correctness. Since all of your exams are on the same day and knowing your teachers will cancel all the exams if he doesn't show up in time, you decide that you must find a way to delay him.
You decide to ask him where he lives, and he gladly obliges. He tells you that he lives in North Bay, Ontario and that he commutes every day to Don Mills C.I., located in Toronto. In addition, you notice that he has a GPS in his car, which provides him with the fastest route but does not receive live traffic updates. This guarantees that he will drive through his original route. In the case where there are multiple fastest routes, his GPS chooses the one that goes through the least number of intersections.
According to a recent study, drivers tend to drive slower when they see a drone-balloon flying over them that has a sign asking them what they ate for breakfast. More specifically, they make the driver reduce their speed by exactly . Taking advantage of this newly-found information, you decide to purchase some drone-balloons from your local drone dealer and fly exactly one over each road he will take.
Also, since drivers are too focused when passing through intersections, flying drone-balloons exactly over intersections has no effect on their speed.
Unfortunately, drones cost money, which means that you wish to fly drone-balloons only over the roads you are sure he will take. You also wish to determine the amount of time the teachers will have to wait for him to show up after cancelling the exams.
Constraints
It is guaranteed that all roads will be of the same distance and have the same speed limit for at least 20% of the test cases.
Note that there may be parallel edges — different roads that travel between the same two intersections.
Input Specification
The first line of input will consist of the number of all the intersections/interchanges in the region,
.
The second line of input will consist of the number of roads or highways in the region,
.
Each of the next lines will contain four integers separated by spaces. The first two,
and
, represent a road/highway from intersection
to
and vice-versa (assume there are no one-way streets).
The last two, and
, represent the distance (km) and the speed limit (km/h) of the road or highway. Assume that the Math Teacher drives exactly at the posted speed limit.
He starts at intersection and that the school is at intersection
. Find the number of drone-balloons required (one for each road he will take) and the time he will be delayed by.
Output Specification
There should be two lines of output, the first one containing the minimum number of drone-balloons required for the shortest path (by time) and the second containing the time he will be delayed by, to the nearest minute.
Sample Input
3
3
1 3 350 80
1 2 200 80
2 3 150 100Sample Output
2
80Explanation for Sample Output
The diagram below is a visual representation of the graph:
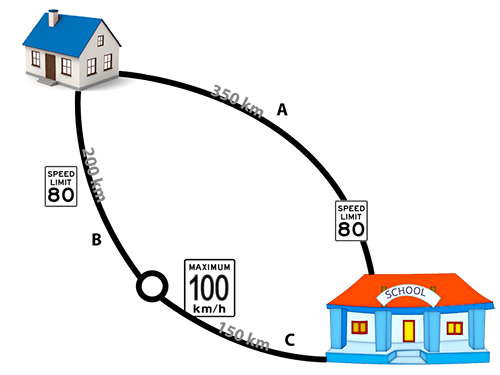
It takes 262.5 minutes to go through A, 150 minutes to go through B, and 90 minutes to drive through C. The fastest path will go through B and C for a total travel time of 240 minutes. Since two roads will be taken, 2 drone-balloons will be required. Moreover, a 25% reduction in speed along each road means that the total travel time will now be 320 minutes. Therefore you delayed him by 80 minutes and succeeded in cancelling the exams.
Comments
What if there are multiple edge-disjoint paths which take the same time and go through the same number of vertices? Then we cannot be sure he will take any of them, so do we output 0?
The output would be the same for both then
Rounding
Am I rounding my final answer incorrectly? Should I round the original time and the slowed time and then subtract, or round after subtracting?
You should round after subtracting.