nitewing was stuck in the never-ending TEJ classes. Being very fast, he finishes all the work the teacher assigned and decides to do some research on operational amplifiers.

nitewing realizes that operational amplifiers have a wide variety of uses. He finds out that an ideal operational amplifier would amplify the difference between the non-inverting input (denoted in the diagram with a +) and the inverting input (denoted in the diagram with a -), with an infinite gain.

nitewing finds out that without a feedback loop, the operational amplifier would only act as a comparator. Since he is only interested in non-inverting amplifiers, he connects the operational amplifier in a negative feedback loop configuration, like so:

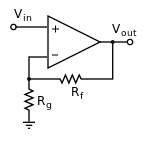
nitewing wants to be able to calculate the output voltage, given the input voltage and the values of the two resistors. He goes on Wikipedia and finds the formula:

~V_{out} = V_{in} \times \left(1 + \frac{R_f}{R_g}\right)~

Since he has other work to do, he leaves this task to you. Can you help him solve this problem?

Assume that the operational amplifiers are ideal and do not saturate.

Input Specification

The first and only line of input will contain ~V_{in}~ ~(-1000 \leq V_{in} \leq 1000)~, ~R_f~ ~(0 \leq R_f \leq 1000)~, ~R_g~ ~(1 \leq R_g \leq 1000)~.

Output Specification

Compute and output the value of ~V_{out}~ for the given ~V_{in}~, ~R_f~ and ~R_g~, using the formula described above.

Your answer will be considered correct if it is within a relative or absolute error of ~10^{-2}~.

Sample Input

3 100 120

Sample Output

5.5

Explanation

The output is obtained by ~3 \times \left(1 + \frac{100}{120}\right)=5.5~.