Editorial for DMOPC '21 Contest 7 P6 - Rainbow Subgraphs
Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.
Submitting an official solution before solving the problem yourself is a bannable offence.
Author:
Subtask 1
Hint
All the points inHint 2
Use broken profile DP.Solution
For subtask 1, note that all the points inTime Complexity:
Subtask 2
Hint
Most of the rectangle is empty. At most how many points are there for eachHint 2
Use this to reduce the number of states in the broken profile DP.Solution
For subtask 2, note that although the rectangle has a height ofWe can analyze the time complexity of this solution as follows. Observe that the maximum number of points sharing the same
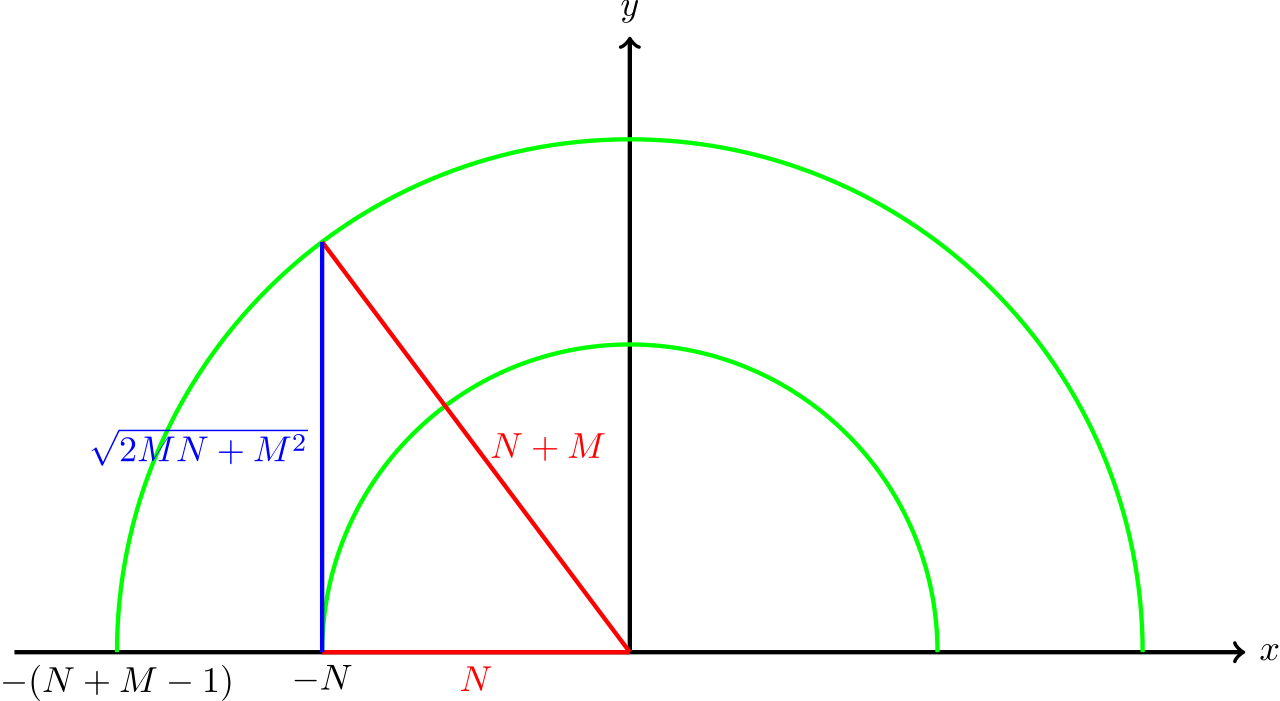
Furthermore, there are only around
Time Complexity:
Subtask 3
Hint
What is the bottleneck of the subtask 2 solution? How can we prevent needing this many states?Hint 2
Note that the horizontal "width" of the rainbow shape is small when the vertical "width" is large.Solution
For subtask 3, consider the bottom-left part of the graph (Case when##############C................................... ##############C######............................. ##############C##########......................... ##############CBBBBBBBBBBBBBB..................... AAAAAAAAAAAAAACAAAAAAAAAAAAAAAAAA................. ...............####################............... ....................##################............ .........................################......... ............................###############....... ................................#############..... ...................................############... .....................................############. ........................................########## ..........................................######## ............................................###### ..............................................#### ................................................## .................................................. .................................................. ..................................................The bottleneck of the subtask 2 solution is the long column at
A's above), causing the profile to get up to size C's in the diagram above. If we knew the state of all the C's, we could use a simpler dynamic programming to find the number of ways to complete the subgraph within this rectangle. We can process the region to the right of the C's and above the B's (in the diagram above) while maintaining a state of which C's are chosen and a profile that doesn't exceed the number of B's in the diagram. After processing this region, we can multiply the current DP value by the number of ways to complete the subgraph within the rectangle and continue with the same broken profile DP as subtask 2 (now that the information about the C's is no longer needed). This idea reduces the maximum necessary size of the profile by about Time Complexity:
Subtask 4
Hint
How can we extend the idea from subtask 3 to further reduce the maximum size of the profile needed?Hint 2
Switch from using horizontal profiles to vertical profiles at the optimum location.Solution
The subtask 3 solution effectively switches between using a horizontal profile and a vertical profile at the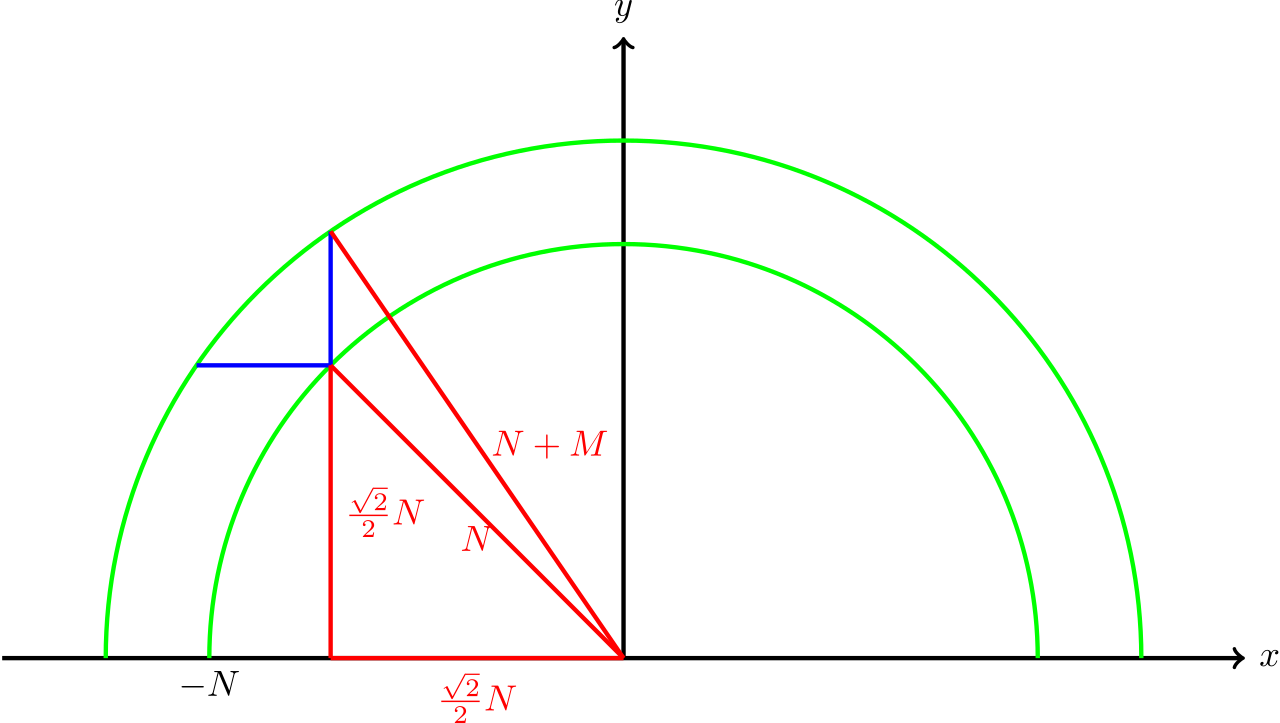
We can calculate the maximum profile size we now need as
Time Complexity:
Subtask 5
Hint
How can we transition more smoothly between a perfectly horizontal profile at the start to a perfectly vertical profile at the middle?Hint 2
The "rainbow" shape has a uniform "thickness" ofHint 3
Instead of sweeping through the rainbow in a linear fashion, sweep through it in an angular fashion.Solution
Instead of "sharply" transitioning between horizontal and vertical profiles, we can instead sweep through the points in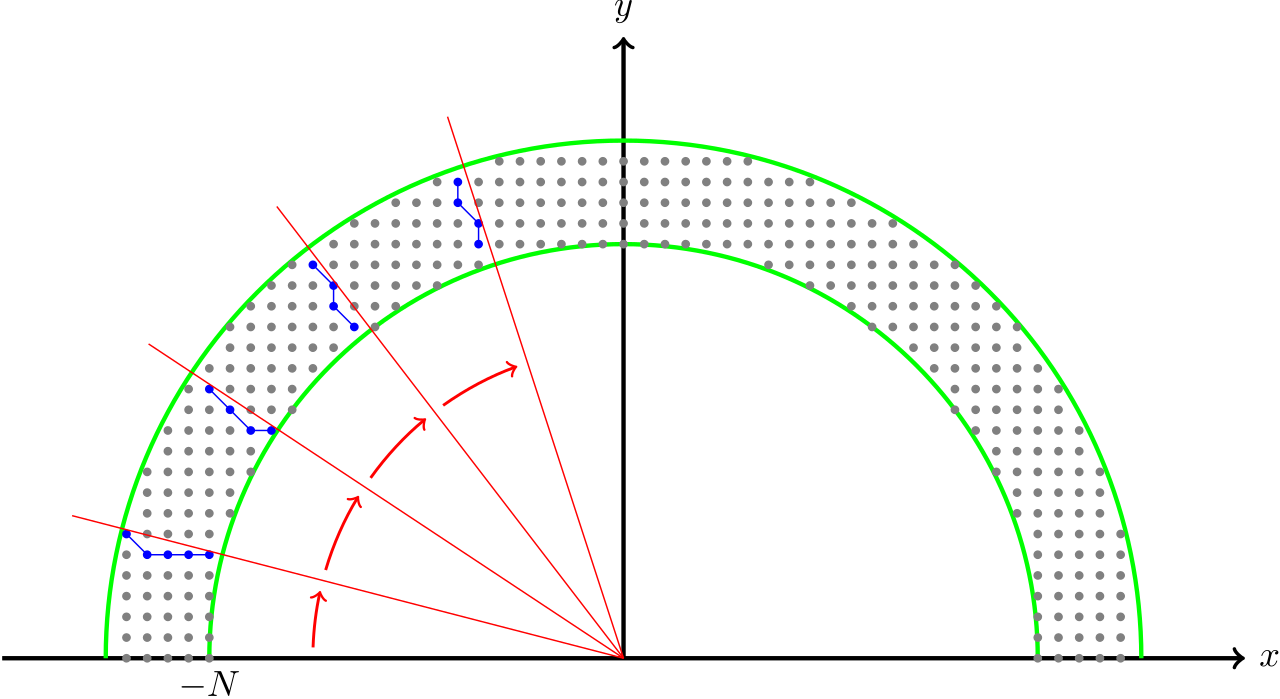
(In fact, the size of the profile gets closer to
When handling the DP transitions, a naive implementation might take
- Replace two consecutive points with one new point.
- Replace one point with a new point.
- Insert a new point at the beginning.
- Insert a new point at the end.
Time Complexity:
Remark: The small "thickness" of the rainbow shape we used in this problem can be viewed as the graph
Comments
The claim in the alternative solution seems wrong? For ,
,  and
and  are connected by an edge but are not always within
are connected by an edge but are not always within  indices of each other.
indices of each other.
I replaced the alternative solution with a remarks section that is hopefully more correct.