Pure brute force is too slow. However, note that we can process all permutations at the beginning. Using a map, we can compute, for each possible input, what secret arrays are possible, and more importantly, which values are constant across all secret arrays.

Flow?

It is known that for each card from ~1~ to ~N~, exactly two, one, or zero people will declare it to be their neighbours' minimum card. Let us consider the following for each card ~K~ from ~1~ to ~N~:

1. If two people claim that the minimum card held by their neighbours is ~K~, then card ~K~ is located between them.

2. If one person claims that the minimum card held by their neighbours is ~K~, then card ~K~ is located in at least one of the spots beside them.

3. If nobody claims that the minimum card held by their neighbours is ~K~, we can theoretically place it anywhere. However, if someone says that the minimum label of their neighbours' cards is ~V~, none of the cards beside them can be strictly less than ~V~. Thus, we can rule out some of the potential places where we could place card ~K~.

Using this information, we can model the problem as a bipartite graph, with each edge denoting a possible location to place the card. Since the information provided always corresponds to some real arrangement of cards, there will always exist at least one perfect bipartite matching. Thus, it suffices to find the set of maximally-matchable edges (edges which exist in at least one perfect bipartite matchings), and place a card in its desired location if it has a unique maximally-matchable outgoing edge.

Luckily for us, there exists an algorithm which can find the set of all maximally-matchable edges in linear time given an existing perfect bipartite matching, outlined in the following article by professor Tamir Tassa in the journal of Theoretical Computer Science. To briefly summarize the algorithm:

1. First, find a maximal bipartite matching. This can be accomplished using any maximum flow or matching algorithm.

2. For each edge in the maximal bipartite matching, label its source node ~X~ and its destination node ~X'~.

3. Build a separate directed graph ~G~ with ~N~ nodes. For each edge in the bipartite graph, not necessarily in the maximal bipartite matching that connects some ~A~ and ~B'~, construct a directed edge from node ~A~ to node ~B~ in graph ~G~.

4. An edge in the bipartite graph that connects some ~A~ and ~B'~ is a maximally-matchable edge if ~A~ and ~B~ are in the same strongly connected component in graph ~G~.

We can place the cards as per the set of maximally-matchable edges to construct our final array: a card has a unique position in the array if it only has one unique maximally-matchable outgoing edge. Remember that ~N = 4~ is a special case and should be coded separately. In the following illustration of ~T=1~ in the sample case, unique maximally-matchable edges are shown in blue, while non-unique maximally-matchable edges are shown in black.

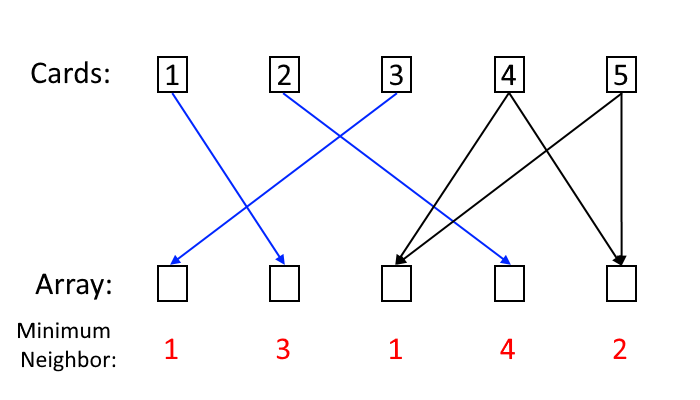
This algorithm's time complexity is dependent on the time complexity of the algorithm used to find the maximal bipartite matching. Any sufficiently fast flow or matching algorithm can be used. However, do be aware that there are around ~N^2~ edges.

Time Complexity: ~\approx \mathcal O(\sum N^2)~

Remark: Pruning unneeded edges ahead of time speeds up the algorithm by a constant factor. Though many unneeded edges were pruned using the strategy in point 3, it is possible to do better. Nonetheless, it is conjectured that the minimum number of edges to be considered in a worst-case scenario will always remain quadratic with respect to ~N~ unless a strategy is adopted akin to the one outlined in the final subtask.

The intended solution is not flow, or anything related to it. It rather has to do with careful processing.

Obviously, if two neighbours of a person say that the minimum element is ~X~, then the position of ~X~ is known.

Furthermore, if we have a configuration like below:

A B C D E

Where ~A < C < E~, then the person between ~C~ and ~A~ must be holding ~C~. Why? Well it cannot be ~A~, otherwise ~C~ would not have been reported. ~C~ cannot be on the other side since ~E > C~, and ~E~ was reported.

Armed with these two observations, what remains to the problem?

Consider a case like 1 2 1 2 4. Given our current rules, our output would be 0 1 2 0 0. The correct output, which you can verify with the subtask ~1~ solution, is 0 1 2 0 3.

Similar to the solution discussed for subtask ~2~, we need to think about when a missing number is guaranteed. Why is the ~3~ guaranteed here? Well, ~4~ and ~5~ have to be on either side of the ~4~, and ~1~ and ~2~ have been placed, so ~3~ has only one spot.

Cases that trigger this issue can get much more complicated. How do we deal with this then?

After applying the initial rules above, for any positions not filled in, we have a lower bound on the value. We also know all values not used. After sorting both lists, we can use what is essentially a two-pointer sweep to determine which positions are uniquely determined. For instance, if the bounds are ~3, 3, 4, 6, 8, 8~ and the unused values are ~3, 4, 5, 7, 8, 9~, then ~7~ is guaranteed.

Full details of the algorithm above are left as an exercise.