DWITE '09 R2 #4 - Breadth First Not Quite Tree

View as PDF
Submit solution
Points: 5
Time limit: 2.0s
Memory limit: 64M
Problem type
DWITE Online Computer Programming Contest, November 2009, Problem 4

In a graph, each node has a "level" – a distance to the root (start) node. One of the special properties that could be extracted, is that if there is a connection between two nodes of the same level, then there is also a cycle of odd length in the graph, which in turn gives us more properties about the structure.

The input will contain 5 test cases: A single positive integer 1≤N≤50, followed by N lines describing the graph. Each line is two integers, IDs of nodes, separated by a space. Node IDs are positive integers less than 100. The root (start) node has ID 1.

The output will contain 5 lines, integer count of how many pairs of nodes have a connection, such that the shortest path from 1 to each node is equal.

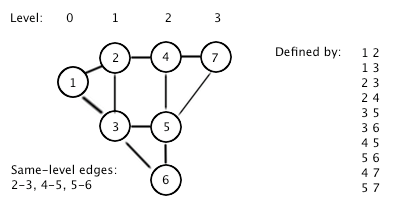
graph of sample input

Sample Input

Copy
3
1 2
3 2
1 3
10
1 2
1 3
2 3
2 4
3 5
3 6
4 5
5 6
4 7
5 7

Sample Output

Copy
1
3

Problem Resource: DWITE

Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported

Comments


  • 1
    rsylshzxdkh  commented on April 19, 2018, 11:25 a.m.

    Question: For the sample input, should not 4 and 6 also be a pair(2 edges from the root)?


    • 0
      devansh289  commented on Aug. 8, 2018, 1:28 a.m.

      Does anyone know?


      • 3
        Jonathan_Uy  commented on May 4, 2020, 1:52 a.m.

        They have to be directly connected (share an edge between them) as well as being on the same level.


  • 8
    TheCool1James  commented on Oct. 21, 2017, 8:58 p.m.

    It should be clarified that in the sample input and output only 2 sets of the 5 are shown


    • 1
      Darcy_Liu  commented on March 31, 2018, 1:22 a.m.

      Got it