DWITE Online Computer Programming Contest, December 2009, Problem 5

One of the ways to print t-shirt designs is by a process called screen printing — a design is broken up into "screens" that allow paint to fill certain solid regions. This results in a higher quality print, but requires additional setup (and thus cost) for every colour used.

Having started what we hope to turn out to be a successful t-shirt design company, we want to minimize the printing costs. Each design can be modeled as a graph, and we want to be able to colour it such that no two adjacent nodes are of the same colour (think of it as a map of countries — every country border has two different colours). What is the minimum number of colours that each design requires? Let's assume that paying for more than 4 is too much, so if we can't colour it in 4, we'll give up.

The input will contain 5 sets of input. First line will contain a positive integer ~1 \le N \le 20~, number of edges in a graph, followed by ~N~ lines describing the graph. Each such line will contain two positive integers, separated by a single space — a connection between two nodes identified by such integers. If both node IDs are the same, treat it as a disconnected node (there is no edge to itself).

The output will contain 5 lines, the minimum number of colours required to colour the graph, or 0 if 4 is not enough.

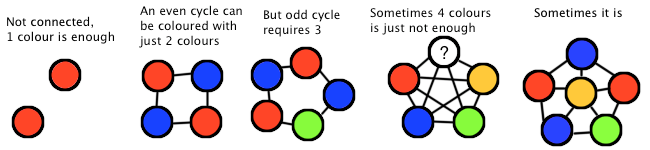
Sample Input

2
1 1
2 2
4
1 2
2 3
3 4
4 1
5
1 2
2 3
3 4
4 5
5 1
10
1 2
2 3
3 4
4 5
5 1
1 3
1 4
2 4
2 5
3 5
10
1 2
2 3
3 4
4 5
5 1
6 1
6 2
6 3
6 4
6 5

Sample Output

1
2
3
0
4

Problem Resource: DWITE