You have a ~10 \times 10~ board made of tiles that are black on one side and light grey on the other, but right now they're all showing their grey side. Imagine the patterns you could make! For example, suppose you imposed a grid over the tiles to divide them into squares of the same size with no tiles left over. There are four grid sizes that would work: ~1 \times 1~, ~2 \times 2~, ~5 \times 5~ and ~10 \times 10~, as shown below (the tiles are in grey, the grids are shown with black lines).

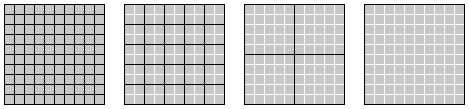
Now imagine that each grid is a checkerboard where the top left square is a black square, like this:

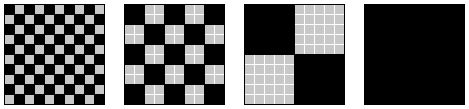
Now imagine flipping over all the tiles that are underneath black grid squares. Do the ~1 \times 1~ grid first, then ~2 \times 2~, then ~5 \times 5~, then ~10 \times 10~. You're going to get some cool patterns. The pictures below show the results.

The input will contain ~10~ test cases. Each test case consists of six lines. The first line contains a single integer ~N~ ~(1 \le N \le 1\,000\,000)~ representing the size of the board. The next ~5~ lines each contain two integers ~R~ and ~C~, separated by a space. ~R~ and ~C~ represent the row and column of a tile on the board ~(1 \le R,C \le N)~. Rows are numbered top down starting at ~1~ and columns are numbered left to right starting at ~1~.

Your job is to simulate the pattern-making process described above for an ~N \times N~ board, and then output a single line of ~5~ characters representing the five tiles in the locations given in the test case, in the order they originally appeared in the file. Each tile should be represented by an uppercase B or G depending on whether it is showing its black or grey side in the final pattern.

Note that there are ~2~ test cases in the sample data below, but the real data files will contain ~10~ test cases.

Sample Input

10
5 1
5 2
5 3
5 4
5 5
12
6 6
7 7
8 8
9 9
10 10

Sample Output

GBBGG
GGGGG

Educational Computing Organization of Ontario - statements, test data and other materials can be found at ecoocs.org