Google Code Jam '22 Round 1C Problem A - Letter Blocks
View as PDFIt is a rainy day, so you are indoors building towers of letter blocks. A letter block is a wooden cube that has a letter printed on one of its sides. The font used for the letters makes the blocks have a clear orientation: that is, there is only one side that can be pointed down (toward the floor) and one side that can be pointed up (toward the ceiling).
You have built multiple separate towers so far. Now you want to combine all of them into a single megatower by choosing one of your towers as the base, then picking up another tower (without changing the order of its blocks) and stacking the whole thing on top of that, and so on, until all towers have been used.
As an additional constraint for the megatower, for any two blocks that have the same letter, all blocks between them must also have that letter. That is, each letter of the alphabet that appears in the megatower needs to appear in one contiguous group (of one or more blocks).
For example, consider the following three possible megatowers. (These are separate examples, not built from the same original towers. Also note that the different block sizes are just for fun and are not part of the problem.)
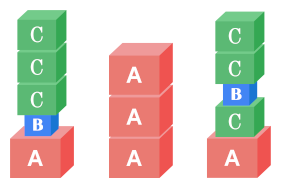
The leftmost two megatowers are valid, since each letter appears in a contiguous group. However, the rightmost megatower is not valid, because there is a B in between two Cs.
Given the towers that you have built so far, can you stack them all up into a valid megatower?
Input Specification
The first line of the input gives the number of test cases, .
test cases follow. Each test case is described by two lines. The first line consists of a single integer
, the number of towers that are currently built. The second line consists of
strings
representing the towers. Each of these strings consists of only uppercase letters. The
letter of each of these strings is the letter on the
block from the bottom in the represented tower.
Output Specification
For each test case, output one line containing Case #x: y, where is the test case number (starting from
) and
is a string representing a valid megatower as described above, or the word
IMPOSSIBLE if no valid megatower can be built. (Notice that the string IMPOSSIBLE can never itself represent a valid megatower, since the two Is have other letters in between.)
Limits
.
, for all
.
Test Set 1
.
Test Set 2
.
Sample Input
6
5
CODE JAM MIC EEL ZZZZZ
6
CODE JAM MIC EEL ZZZZZ EEK
2
OY YO
2
HASH CODE
6
A AA BB A BA BB
2
CAT TAXSample Output
Case #1: ZZZZZJAMMICCODEEEL
Case #2: IMPOSSIBLE
Case #3: IMPOSSIBLE
Case #4: IMPOSSIBLE
Case #5: BBBBBAAAAA
Case #6: IMPOSSIBLEExplanation for Sample
In Sample Case #1, JAMMICCODEEELZZZZZ and ZZZZZJAMMICCODEEEL are the only two valid outputs.
In Sample Case #2, recall that all towers must be used in the megatower, so even though the first five towers together would form a valid megatower (as in Sample Case #1), the additional EEK makes the case impossible. No matter how the EEL and EEK towers are stacked relative to each other, there will be at least two non-contiguous groups of Es.
In Sample Case #3, no matter how you stack the towers, either the two Os are not contiguous or the two Ys are not contiguous.
In Sample Case #4, there are non-H letters in between the Hs of HASH, so this case is also impossible.
In Sample Case #5, this answer is the only valid one. Also notice that the towers are not necessarily all distinct.
In Sample Case #6, no matter how you stack the towers, the two As cannot be contiguous.
Comments