Addition and squaring do not commute. That is, the square of the sum of all elements of a list of integers is not necessarily equal to the sum of the squares of those same elements. However, this is true for some lists; one example is $[3,-2,6]$, because $(3+(-2)+6{)}^2=49=3^2+(-2{)}^2+6^2$. Let us call these lists squary.

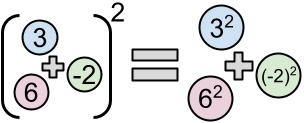
Given a (not necessarily squary) list of relatively small integers, we want to know whether it is possible to add at least $1$ and at most $K$ more elements such that the final list is squary. Each added element must be an integer between $-{10}^{18}$ and ${10}^{18}$, inclusive, and these do not have to be distinct from each other or from the initial list's elements.

Input Specification

The first line of the input gives the number of test cases, $T$. $T$ test cases follow. Each test case is described in two lines. The first line contains two integers $N$ and $K$, the number of elements of the initial list and the maximum number of elements you may add, respectively. The second line contains $N$ integers $E_1,E_2,\dots ,E_N$, representing the $N$ elements of the initial list.

Output Specification

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from $1$). If it is possible to add at least $1$ and at most $K$ elements (each an integer between $-{10}^{18}$ and ${10}^{18}$, inclusive) to the initial list such that the square of the sum of its elements equals the sum of the squares of its elements, $y$ should be $z_1{z}_2\dots z_r$, where $1\le r\le K$ and the $z_i$ values are the additional elements. If there is no way to accomplish this, $y$ should be IMPOSSIBLE.

Limits

$1\le T\le 100$.

$1\le N\le 1000$.

$-1000\le E_i\le 1000$, for all $i$.

Test Set 1

Time limit: 5 seconds.

$K=1$.

Test Set 2

Time limit: 10 seconds.

$2\le K\le 1000$.

Sample Input 1

4
2 1
-2 6
2 1
-10 10
1 1
0
3 1
2 -2 2

Sample Output 1

Case #1: 3
Case #2: IMPOSSIBLE
Case #3: -1000000000000000000
Case #4: 2

Explanation for Sample 1

This Sample corresponds to the constraints of Test Set 1 and 2.

In Sample Case #1, we can end up with the example list given in the problem statement.

In Sample Case #2, we have to add exactly one element. If we call that element $x$, the sum of the entire list is $x$ and its square is $x^2$. The sum of the squares of all elements, on the other hand, is $x^2+{10}^2+(-10{)}^2=x^2+200\ne x^2$, so the case is impossible.

In Sample Case #3, any integer in the $[-{10}^{18},{10}^{18}]$ range is a valid answer.

In Sample Case #4, notice that the input might contain duplicate elements, and that it is valid to create even more duplicates with the elements you choose to add.

Sample Input 2

3
3 10
-2 3 6
6 2
-2 2 1 -2 4 -1
1 12
-5

Sample Output 2

Case #1: 0
Case #2: -1 15
Case #3: 1 1 1 1 1 1 1 1 1 1 1

Explanation for Sample 2

This Sample corresponds to the constraints of Test Set 2.

In Case #1 of the additional samples, we are given the example list from the problem statement, which is already squary, but we need to add at least one element to it. Adding a $0$ keeps the list squary.

In Case #3 of the additional samples, we present one of multiple possible valid answers. Notice that it is permissible to add fewer than $K$ elements; here $K$ is $12$ but we have only added $11$ elements.

Note

This problem has different time limits for different batches. If you exceed the Time Limit for any batch, the judge will incorrectly display >10.000s regardless of the actual time taken. Refer to the Limits section for batch-specific time limits.